
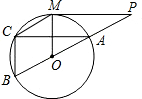
 如图,MP切⊙O于点M,直线PO交⊙O于点A,B,弦AC∥MP,当PA,AO满足什么条件时,四边形BOMC为菱形?并说明理由.
如图,MP切⊙O于点M,直线PO交⊙O于点A,B,弦AC∥MP,当PA,AO满足什么条件时,四边形BOMC为菱形?并说明理由. 分析 根据切线的性质得OM⊥PM,而AC∥MP,所以OM⊥AC,再由圆周角定理得∠ACB=90°,所以OM∥BC,当PA=OA时可证明△ABC≌△POM,则OM=BC,于是可判断四边形BOMC为平行四边形,加上OB=OM,则可判断四边形BOMC为菱形.
解答 解:PA=AO时,四边形BOMC为菱形.理由如下:
∵MP切⊙O于点M,
∴OM⊥PM,
∵AC∥MP,
∴OM⊥AC,
∵AB为直径,
∴∠ACB=90°,
∴OM∥BC,
∴∠B=∠MOP,
∵PA=OA,
∴AB=OP,
在△ABC和△POM中,
$\left\{\begin{array}{l}{∠ACB=∠PMO}\\{∠ABC=∠POM}\\{AB=PO}\end{array}\right.$,
∴△ABC≌△POM,
∴OM=BC,
∴四边形BOMC为平行四边形,
而OB=OM,
∴四边形BOMC为菱形.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了菱形的判定.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+(-1)=1+2 | B. | 3+(-2)+5=(-2)+3+5 | ||
| C. | [6+(-3)]+5=[6+(-5)]+3 | D. | $\frac{1}{3}$+(-2)+(+$\frac{2}{3}$)=($\frac{1}{3}$+$\frac{2}{3}$)+(+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com