
 (x>0);③
(x>0);③ (x>0);在给定自变量x的取值范围内,是增函数的有______.
(x>0);在给定自变量x的取值范围内,是增函数的有______. (x>0),
(x>0), (x>0),
(x>0), =-
=- =1,
=1,

科目:初中数学 来源: 题型:解答题
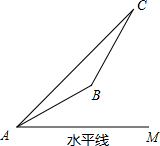 车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(
车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(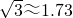 ,精确到1米)
,精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于点E,∠POC=∠PCE.
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于点E,∠POC=∠PCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 销量.我市某家电公司营销点对自去年10月份至今年3月份销售两种不同品牌冰箱的数量做出统计,数据如图所示:
销量.我市某家电公司营销点对自去年10月份至今年3月份销售两种不同品牌冰箱的数量做出统计,数据如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com