
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.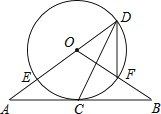
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
【答案】
(1)
①证明:连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB,
∵点C在⊙O上,
∴AB是⊙O切线.
②证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC,
∵OD=OF,
∴∠ODF=∠OFD,
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC=∠CDF
(2)
解:作ON⊥DF于N,延长DF交AB于M.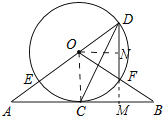
∵ON⊥DF,
∴DN=NF=3,
在RT△ODN中,∵∠OND=90°,OD=5,DN=3,
∴ON= ![]() =4,
=4,
∵∠OCM+∠CMN=180°,∠OCM=90°,
∴∠OCM=∠CMN=∠MNO=90°,
∴四边形OCMN是矩形,
∴ON=CM=4,MN=OC=5,
在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,
∴CD= ![]() =
= ![]() =4
=4 ![]() .
.
【解析】(1)①欲证明直线AB是⊙O的切线,只要证明OC⊥AB即可.②首先证明OC∥DF,再证明∠FDC=∠OCD,∠EDC=∠OCD即可;
(2)作ON⊥DF于N,延长DF交AB于M,在RT△CDM中,求出DM、CM即可解决问题.本题考查切线的判定,等腰三角形的性质、垂径定理、平行线的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】有 20 筐白菜,以每筐 25 千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)与标准质量比较,20 筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价 2 .6 元,则出售这 20 筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.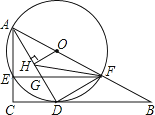
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2 ![]() ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为 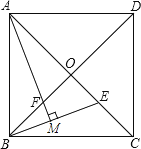
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8 分)2013 年 4 月起泉州市区居民生活用水开始实行阶梯式计量水价,据了解,此次实行的阶梯式计量水价分为三级(如表所示):

例:若某用户 2013 年 6 月份的用水量为 35 吨,按三级计算则应交水费为:
20×1.65+(30﹣20)×2.48+(35﹣30)×3.30=74.3(元)
(1)如果小东家 2013 年 6 月份的用水量为 20 吨,则需缴交水费多少元?
(2)如果小明家 2013 年 7 月份的用水量为 a 吨,水价要按两级计算,则小明家该月应缴交水费多少元?(用含 a 的代数式表示,并化简)
(3)若一用户 2013 年 7 月份应该水费 90.8 元,则该户人家 7 月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中![]() 直线
直线![]() 与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转
与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转![]() 得到CD,此时点D恰好落在直线AB上时,过点D作
得到CD,此时点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 如图2,将
如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;
![]() 若点P在y轴上,点Q在直线AB上
若点P在y轴上,点Q在直线AB上![]() 是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.
是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(AB<BC)的对角线交点O旋转(如图①→②→③),图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.
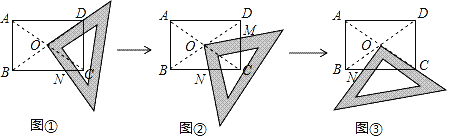
(1)该学习小组中一名成员意外地发现:在图①(三角板的一直角边与OD重合)中,BN2=CD2+CN2;在图③(三角板的一直角边与OC重合)中,CN2=BN2+CD2.请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的关系,写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com