
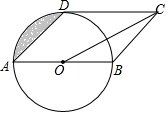
 如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2. 分析 如图连接OD.在Rt△ODC中,利用勾股定理求出OD,根据S阴=S扇形OAD-S△AOD计算即可.
解答 解:如图连接OD.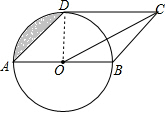
∵CD是⊙O的切线,
∴OD⊥CD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB⊥OD,设OD=r,则CD=AB=2r,
∴∠AOD=∠ODC=90°,
在Rt△OCD中,∵OC2=OD2+CD2,
∴(2$\sqrt{5}$)2=r2+(2r)2,
∴r=2,
∴S阴=S扇形OAD-S△AOD=$\frac{90•π•{2}^{2}}{360}$-$\frac{1}{2}$•2•2=π-2.
故答案为π-2.
点评 本题考查切线的性质、平行四边形的性质、扇形的面积公式、勾股定理等知识,解题的关键是确定圆心角的度数以及半径,属于中考常考题型.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC.若AB=m,AD=n,则四边形OCED的面积为( )| A. | mn | B. | $\frac{1}{2}$mn | C. | $\frac{1}{4}$mn | D. | $\sqrt{mn}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
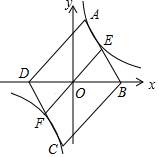 如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
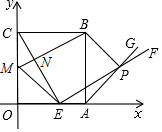 如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
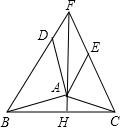 如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形.
如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
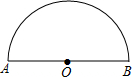 如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )| A. | 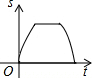 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
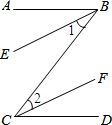 (1)完成下面的推理说明:
(1)完成下面的推理说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
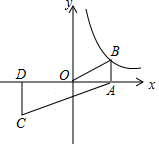 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com