
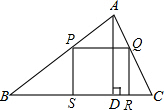
 一块铁皮呈锐角三角形,它的一边BC=80cm,高AD=60cm.要把它加工成矩形零件PQRS,使矩形的一边SR位于边BC上,另两个顶点P、Q分别在边AB、AC上,请你设计一个加工方案,使矩形零件的面积最大,并求出最大面积.
一块铁皮呈锐角三角形,它的一边BC=80cm,高AD=60cm.要把它加工成矩形零件PQRS,使矩形的一边SR位于边BC上,另两个顶点P、Q分别在边AB、AC上,请你设计一个加工方案,使矩形零件的面积最大,并求出最大面积. 分析 根据题意得出△APQ∽△ABC,进而表示出PQ的长,再利用二次函数最值求法得出答案.
解答 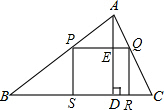 解:PQ与AD交于点E,如图,设QR=xcm,
解:PQ与AD交于点E,如图,设QR=xcm,
易得四边形QRSP为矩形,则ED=QR=x,
则AE=AD-ED=60-x,
∵PQ∥BC,
∴△APQ∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PQ}{BC}$,即$\frac{60-x}{60}$=$\frac{PQ}{120}$,
∴PQ=2(60-x),
∴S矩形PQMN=PQ•QR=2(60-x)•x=-2(x-30)2+1800,
当x=30时,S矩形PQRS,有最大值,最大值为1800(cm2).
答:要使加工成的这个矩形面积最大,那么边长QR应是30cm.
点评 本题考查了相似三角形的应用以及二次函数的最值问题,根据题意表示出PQ的长是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com