
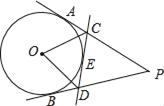
【题目】如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的个数为( )
A. 3个 B. 2个 C. 1个 D. 0个
【答案】B
【解析】
根据切线长定理,可判断①正确;将△PCD的周长转化为PA+PB,可判断②错误;连接OA、OB、OE,求出∠AOB,再由∠COD=∠COE+∠EOD=![]() (∠AOE+∠BOE)=
(∠AOE+∠BOE)=![]() ∠AOB,可判断③正确;
∠AOB,可判断③正确;
解:∵PA、PB是⊙O的切线,
∴PA=PB,故①正确;
∵PA、PB、CD是⊙O的切线,
∴CA=CE,DE=DB,
∴△PCD的周长=PC+CE+DE+PD=PC+CA+PD+DB=PA+PB=2PA=10,故②错误;
连接OA、OB、OE,
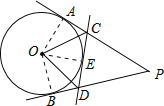
∠AOB=180°-∠APB=140°,
∴∠COD=∠COE+∠EOD=![]() (∠AOE+∠BOE)=
(∠AOE+∠BOE)=![]() ∠AOB=70°,故③正确.
∠AOB=70°,故③正确.
综上可得①③正确,共2个.
故选B.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
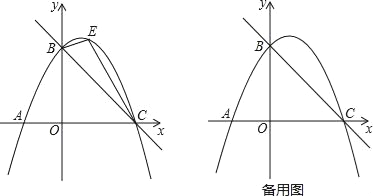
【题目】如图,直线y=﹣2x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片BDEF和直角三角板BCA,点A在EF上,AC=DE=![]() ,FE=3
,FE=3![]() ,∠C=90°,∠CBA=30°.
,∠C=90°,∠CBA=30°.
(1)写出三种不同类型的结论.
(2)将直角三角板绕点B旋转,在旋转过程中,
①求点A与点E的最短距离;
②若将直角三角板绕点B从①中位置开始顺时针旋转α度(0≤α≤360),使∠BAE=90°,求α的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
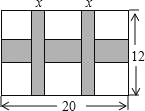
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°,
(1)请判断CD是否⊙O的切线?并说明理由;
(2)若⊙O的半径为6,求弧AC的长.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,∠B=50°,∠A=26°,将△ABC沿DE折叠,点A的对应点是点A′,则∠AEA′的度数是( )

A. 145° B. 152° C. 158° D. 160°
查看答案和解析>>
科目:初中数学 来源: 题型:
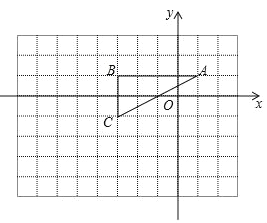
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1)、B(﹣3,1)、C(﹣3.﹣1)
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_____.
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A′、B′、C′,得到△A′B′C′,在图中画出△A′B′C′;若将△A′B′C′沿x轴方向平移,需平移_____单位长度,能使得B′C′所在的直线与⊙P相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com