
分析 (1)根据已知新定义计算即可确定出结果;
(2)观察阅读材料中偶的计算方法,确定出结果即可;
(3)根据题中的新定义作出猜想即可.
解答 解:(1)①∵34=81,
∴log381=4;
②∵100=1,
∴log101=0;
③∵24=16,
∴x=2;
故答案为:4;0;2;
(2)结合题意的分析,可知logaM1M2M3…Mn=logaM1+logaM2+…+logaMn;
故答案为:logaM1+logaM2+…+logaMn;
(3)∵logaMN=logaM+logaN,
∴可猜想:loga$\frac{M}{N}$=logaM-logaN(a>0,a≠1,M、N均为正数).
故答案为:logaM-logaN
点评 此题考查了整式的混合运算,弄清题中的新定义是解本题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
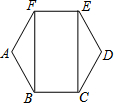 如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为( )
如图,在正六边形ABCDEF中,四边形BCEF的面积为30,则正六边形ABCDEF的面积为( )| A. | 20$\sqrt{3}$ | B. | 40 | C. | 20$\sqrt{5}$ | D. | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
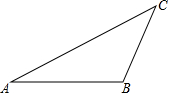 如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):
如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为24.
在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为24.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com