
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为每秒1个单位,过点P作PE⊥AO交AB于点E,一点到达,另一点即停.设点P的运动时间为t秒(t>0).
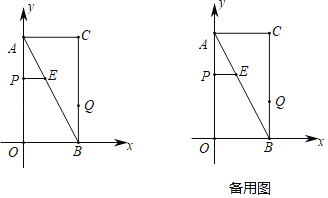
(1)填空:用含t的代数式表示下列各式:AP=______,CQ=_______.
(2)①当PE=![]() 时,求点Q到直线PE的距离.
时,求点Q到直线PE的距离.
②当点Q到直线PE的距离等于![]() 时,直接写出t的值.
时,直接写出t的值.
(3)在动点P、Q运动的过程中,点H是矩形AOBC(包括边界)内一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出点H的横坐标.
【答案】(1)t,4﹣t;(2)①点Q到直线PE的距离为2;②t的值为![]() 秒或
秒或![]() 秒;(3)点H的横坐标为
秒;(3)点H的横坐标为![]() 或10﹣4
或10﹣4![]() .
.
【解析】
(1)由点C坐标及矩形的性质可得出OA=BC=4,OB=AC=2,AO⊥OB,由题意得AP=t,BQ=t,得出CQ=BC﹣BQ=4﹣t;
(2)①延长PE交BC于F,则PF⊥BC,CF=AP=t,由PE⊥AO可得四边形APFC是矩形,可证明PE//OB,可得△APE∽△AOB,得出![]() ,解得t=1,得出BQ=1,CF=1,CQ=3,求出FQ=CQ﹣CF=2即可;
,解得t=1,得出BQ=1,CF=1,CQ=3,求出FQ=CQ﹣CF=2即可;
②延长PE交BC于F,则PF⊥BC,CF=AP=t,当Q在P的下方时,由题意得t+![]() +t=4,解得t=
+t=4,解得t=![]() ;当Q在P的上方时,由题意得t+t-
;当Q在P的上方时,由题意得t+t-![]() =4,解得t=
=4,解得t=![]() .
.
(3)由PE//OB,可得△APE∽△AOB,根据相似三角形的性质可求出E(![]() t,4﹣t),Q(2,t),①当QE=BQ时,延长PE交BC于F,则PF⊥BC,CF=AP=t,则(2﹣
t,4﹣t),Q(2,t),①当QE=BQ时,延长PE交BC于F,则PF⊥BC,CF=AP=t,则(2﹣![]() t)2+(4﹣2t)2=t2,解得t=
t)2+(4﹣2t)2=t2,解得t=![]() ,或t=4(舍去),得出
,或t=4(舍去),得出![]() t=
t=![]() 即可;
即可;
②当BQ=EB时,则BE=BQ=t,利用勾股定理可得AB=2![]() ,由△APE∽△AOB,得出
,由△APE∽△AOB,得出![]() =
=![]() ,求出AE=
,求出AE=![]() t,得出BE=AB﹣AE=2
t,得出BE=AB﹣AE=2![]() ﹣
﹣![]() t,解得t=20﹣8
t,解得t=20﹣8![]() ,即可得出答案.
,即可得出答案.
(1)∵矩形AOBC的顶点C的坐标是(2,4),
∴OA=BC=4,OB=AC=2,AO⊥OB,
∵点P、Q的运动速度均为每秒1个单位,
∴AP=t,BQ=t,
∴CQ=BC﹣BQ=4﹣t;
故答案为:t,4﹣t
(2)①如图1,延长PE交BC于F,
∵PE⊥OA,∠OAC=∠ACB=90°,
∴四边形APFC是矩形,
∴PF⊥BC,CF=AP=t,
∵PE⊥AO,AO⊥OB,
∴PE∥OB,
∴△APE∽△AOB,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:t=1,
∴BQ=1,CF=1,
∴CQ=4﹣1=3,
∴FQ=CQ﹣CF=2;即点Q到直线PE的距离为2.
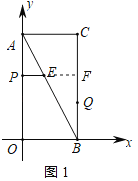
②延长PE交BC于F,则PF⊥BC,CF=AP=t,QF=![]() ,
,
①如上图1,当Q在P的下方时,
由题意得:CF+FQ+BQ=BC=4,即t+![]() +t=4,
+t=4,
解得:t=![]() ;
;
②当Q在P的上方时,如图2所示:
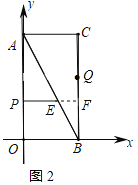
由题意得:BQ+CF-QF=BC,即t+t-![]() =4,
=4,
解得:t=![]() ,
,
∴当点Q到直线PE的距离等于![]() 时,t的值为
时,t的值为![]() 秒或
秒或![]() 秒.
秒.
(3)∵PE⊥AO,AO⊥OB,
∴PE∥OB,
∴△APE∽△AOB,
∴![]() ,即
,即![]() ,
,
解得:PE=![]() t,
t,
∵OP=4﹣t,
∴E(![]() t,4﹣t),Q(2,t),
t,4﹣t),Q(2,t),
①如图3,当QE=BQ时,四边形EQBH是菱形,EH//BQ//y轴,
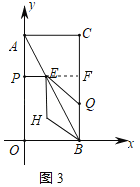
延长PE交BC于F,则PF⊥BC,CF=AP=t,FQ=BC-CF-BQ=4-2t,EF=PF-PE=2-![]() t,
t,
∴(2﹣![]() t)2+(4﹣2t)2=t2,
t)2+(4﹣2t)2=t2,
解得:t=![]() ,或t=4(舍去),
,或t=4(舍去),
∴![]() t=
t=![]() ,
,
∵EH//BQ//y轴,
∴点H的横坐标为![]() ,
,
②如图4,当BQ=EB时,四边形BQHE是菱形,则BE=BQ=t,EH//BQ//y轴,
∵∠AOB=90°,OB=2,OA=4,
∴AB=![]() =2
=2![]() ,
,
∵△APE∽△AOB,
∴![]() ,即
,即![]()
∴AE=![]() t,
t,
∴BE=AB﹣AE=2![]() ﹣
﹣![]() t,
t,
∴2![]() ﹣
﹣![]() t=t,
t=t,
解得:t=20﹣8![]() ,
,
∴![]() t=4=10﹣4
t=4=10﹣4![]() ,
,
∵EH//BQ//y轴,
∴点H的横坐标为10﹣4![]() ,
,

综上所述,点H的横坐标为![]() 或10﹣4
或10﹣4![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
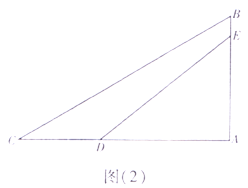
【题目】港珠澳大桥是中国境内一座连接香港、珠海和澳门的桥隧工程,位于中国广东省伶仃洋区域内,为珠江三角洲地区环线高速公路南环段,青州航道桥“中国结三地同心”主题的斜拉索塔如图(1)所示.某数学兴趣小组根据材料编制了如下数学问题,请你解答.
如图(2),BC,DE为主塔AB(主塔AB与桥面AC垂直)上的两条钢索,桥面上C、D两点间的距离为16m,主塔上A、E两点的距离为18.4m,已知BC与桥面AC的夹角为30°,DE与桥面AC的夹角为38°。求主塔AB的高.(结果精确到1米,参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.
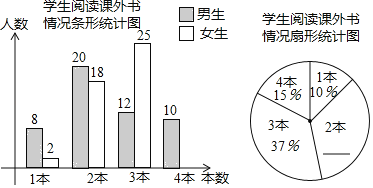
请根据图中信息解决下列问题:
(1)共有多少名同学参与问卷调查;
(2)补全条形统计图和扇形统计图;
(3)全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
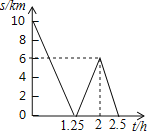
【题目】一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②出发1.25h后两人相遇:③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min时两人相距2km.其中正确的有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
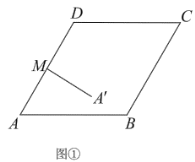
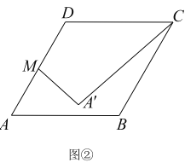
【题目】在边长为2的菱形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,若线段
边的中点,若线段![]() 绕点
绕点![]() 旋转得线段
旋转得线段![]() ,
,
(Ⅰ)如图①,线段![]() 的长__________.
的长__________.
(Ⅱ)如图②,连接![]() ,则
,则![]() 长度的最小值是__________.
长度的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
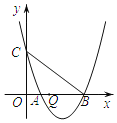
【题目】如图,抛物线y=![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com