
ЁОЬтФПЁПИлжщАФДѓЧХЪЧжаЙњОГФквЛзљСЌНгЯуИлЁЂжщКЃКЭАФУХЕФЧХЫэЙЄГЬЃЌЮЛгкжаЙњЙуЖЋЪЁСциъбѓЧјгђФкЃЌЮЊжщНШ§НЧжоЕиЧјЛЗЯпИпЫйЙЋТЗФЯЛЗЖЮЃЌЧржнКНЕРЧХЁАжаЙњНсШ§ЕиЭЌаФЁБжїЬтЕФаБРЫїЫўШчЭМЃЈ1ЃЉЫљЪО.ФГЪ§бЇаЫШЄаЁзщИљОнВФСЯБржЦСЫШчЯТЪ§бЇЮЪЬтЃЌЧыФуНтД№.
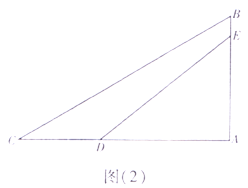
ШчЭМЃЈ2ЃЉЃЌBCЃЌDEЮЊжїЫўABЃЈжїЫўABгыЧХУцACДЙжБЃЉЩЯЕФСНЬѕИжЫїЃЌЧХУцЩЯCЁЂDСНЕуМфЕФОрРыЮЊ16mЃЌжїЫўЩЯAЁЂEСНЕуЕФОрРыЮЊ18.4mЃЌвбжЊBCгыЧХУцACЕФМаНЧЮЊ30ЁуЃЌDEгыЧХУцACЕФМаНЧЮЊ38ЁуЁЃЧѓжїЫўABЕФИп.ЃЈНсЙћОЋШЗЕН1УзЃЌВЮПМЪ§ОнЃКsin38ЁуЁж0.6ЃЌcos38ЁуЁж0.8ЃЌtan38ЁуЁж0.8ЃЌ![]() Ёж1.7ЃЉ
Ёж1.7ЃЉ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдкОиаЮ ABCD жаЃЌЖЏЕу E ДгЕу A ГіЗЂЃЌби ABЁњBC ЗНЯђдЫЖЏЃЌЕБЕу E ЕНДяЕу C ЪБ ЭЃжЙдЫЖЏЃЎЙ§Еу E зї FEЁЭAEЃЌНЛ CD гк F ЕуЃЌЩшЕу E дЫЖЏТЗГЬЮЊ xЃЌFCЃНyЃЌЭМЂкБэЪО yгы x ЕФКЏЪ§ЙиЯЕЕФДѓжТЭМЯёЃЌдђОиаЮ ABCD ЕФУцЛ§ЪЧЃЈ ЃЉ

A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцФкгЩМЋЕуЁЂМЋжсКЭМЋОЖзщГЩЕФзјБъЯЕНазіМЋзјБъЯЕЃЎШчЭМЃЌдкЦНУцЩЯШЁЖЈвЛЕуOГЦЮЊМЋЕуЃЛДгЕуOГіЗЂв§вЛЬѕЩфЯпOxГЦЮЊМЋжсЃЛЯпЖЮOPЕФГЄЖШГЦЮЊМЋОЖЃЎЕуPЕФМЋзјБъОЭПЩвдгУЯпЖЮOPЕФГЄЖШвдМАДгOxзЊЖЏЕНOPЕФНЧЖШЃЈЙцЖЈФцЪБеыЗНЯђзЊЖЏНЧЖШЮЊе§ЃЉРДШЗЖЈЃЌМДPЃЈ3ЃЌ60ЁуЃЉЛђPЃЈ3ЃЌЉ300ЁуЃЉЛђPЃЈ3ЃЌ420ЁуЃЉЕШЃЌдђЕуPЙигкЕуOГЩжааФЖдГЦЕФЕуQЕФМЋзјБъБэЪОВЛе§ШЗЕФЪЧЃЈ ЃЉ
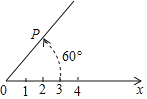
A. QЃЈ3ЃЌ240ЁуЃЉ B. QЃЈ3ЃЌЉ120ЁуЃЉ C. QЃЈ3ЃЌ600ЁуЃЉ D. QЃЈ3ЃЌЉ500ЁуЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉНтВЛЕШЪНзщЃК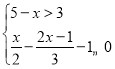
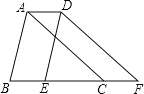
ЃЈ2ЃЉШчЭМЃЌНЋЁїABCбиBCЗНЯђЦНвЦ2cmЕУЕНЁїDEFЃЌШєЁїABCЕФжмГЄЮЊ16cmЃЌЧѓЫФБпаЮABFDЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
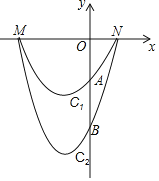
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпC1гыХзЮяЯпC2гыxжсгаЯрЭЌЕФНЛЕуMЃЌNЃЈЕуMдкЕуNЕФзѓВрЃЉЃЌгыxжсЕФНЛЕуЗжБ№ЮЊAЃЌBЃЌЧвЕуAЕФзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЌХзЮяЯпC2ЕФНтЮіЪНЮЊyЃНmx2+4mxЉ12mЃЈmЃО0ЃЉЃЎ
ЃЈ1ЃЉЧѓMЃЌNСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉдкЕкШ§ЯѓЯоФкЕФХзЮяЯпC1ЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЁїPAMЕФУцЛ§зюДѓЃЌШєДцдкЃЌЧѓГіЁїPAMЕФУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшХзЮяЯпC2ЕФЖЅЕуЮЊЕуDЃЌЫГДЮСЌНгAЃЌDЃЌBЃЌNЃЌШєЫФБпаЮADBNЪЧЦНааЫФБпаЮЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDЃЌADЃН4ЃЌABЃН3ЃЌШчЙћЕуEдкБпBCЩЯЃЌНЋжНЦЌбиAEелЕўЃЌЪЙЕуBТфдкЕуFДІЃЌСЊНсFCЃЌЕБЁїEFCЪЧжБНЧШ§НЧаЮЪБЃЌФЧУДBEЕФГЄЮЊ( )

A. 1.5B. 3
C. 1.5Лђ3D. гаСНжжЧщПівдЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2ЃЋbxЃЋ5гыxжсНЛгкЕуA(1ЃЌ0)КЭЕуB(5ЃЌ0)ЃЌЖЅЕуЮЊMЃЎЕуCдкxжсЕФИКАыжсЩЯЃЌЧвACЃНABЃЌЕуDЕФзјБъЮЊ(0ЃЌ3)ЃЌжБЯпlОЙ§ЕуCЁЂDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуPЪЧжБЯпlдкЕкШ§ЯѓЯоЩЯЕФЕуЃЌСЊНсAPЃЌЧвЯпЖЮCPЪЧЯпЖЮCAЁЂCBЕФБШР§жаЯюЃЌ
ЧѓtanЁЯCPAЕФжЕЃЛ
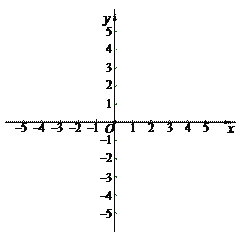
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЊНсAMЁЂBMЃЌдкжБЯпPMЩЯЪЧЗёДцдкЕуEЃЌЪЙЕУЁЯAEM=ЁЯAMB.ШєДцдкЃЌЧѓГіЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
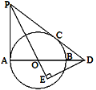
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌPAЁЂPCгыЁбOЗжБ№ЯрЧагкЕуAЃЌCЃЌPCНЛABЕФбгГЄЯпгкЕуDЃЌDEЁЭPOНЛPOЕФбгГЄЯпгкЕуEЃЎ
(1)ЧѓжЄЃКЁЯEPD=ЁЯEDOЃЛ
(2)ШєPC=3ЃЌtanЁЯPDA=![]() ЃЌЧѓOEЕФГЄЃЎ
ЃЌЧѓOEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
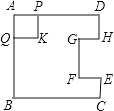
ЁОЬтФПЁП ШчЭМЃЌдкБпГЄЮЊ4ЕФе§ЗНаЮжНЦЌABCDжаЃЌДгБпCDЩЯМєШЅвЛИіОиаЮEFGHЃЌЧвгаEFЃНDHЃНCEЃН1cmЃЌFGЃН2cmЃЌЖЏЕуPДгЕуAПЊЪМбиADБпЯђЕуDвд1cm/sЕФЫйЖШдЫЖЏжСЕуDЭЃжЙЃЎвдAPЮЊБпдкAPЕФЯТЗНзіе§ЗНаЮAQKPЃЌЩшЕуPдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌе§ЗНаЮAQKPКЭжНЦЌжиЕўВПЗжЕФУцЛ§ЮЊSЃЈcm2ЃЉЃЌдђSгыtжЎМфЕФКЏЪ§ЙиЯЕгУЭМЯѓБэЪОДѓжТЪЧЃЈЁЁЁЁЃЉ
A. 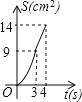 B.
B. 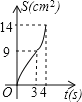
C. 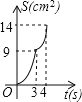 D.
D. 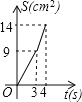
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com