
【题目】已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;
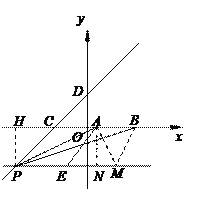
(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
【答案】 (1)![]() ;(2)
;(2) ![]() ;(3)E的坐标为(-2,-4)或(4,-4).
;(3)E的坐标为(-2,-4)或(4,-4).
【解析】试题分析:(1)把A、B两点带入抛物线解析式,求得a、b的值,即可得到抛物线解析式;
(2)由AC=AB且点C在点A的左侧,及线段CP是线段CA、CB的比例中项,可得CP=![]() ,
,
由两边对应成比例且夹角相等的三角形相似,可得△CPA∽△CBP,由此∠CPA= ∠CBP.
过P作PH⊥x轴于H,易得PH=4,H(-7,0),BH=12. 由于P(-7,-4),可求![]() ;
;
(3)分两种情况:点E在M左侧和点E在M右侧讨论即可.
试题解析:(1)∵ 抛物线![]() 与x轴交于点A(1,0),B(5,0),
与x轴交于点A(1,0),B(5,0),
∴![]() ,
,
解得![]()
∴ 抛物线的解析式为![]() .
.
(2)∵ A(1,0),B(5,0),
∴ OA=1,AB=4.
∵ AC=AB且点C在点A的左侧,
∴ AC=4 .
∴ CB=CA+AB=8.
∵ 线段CP是线段CA、CB的比例中项,
∴ ![]() .
.
∴ CP=![]() .
.
又 ∵ ∠PCB是公共角,
∴ △CPA∽△CBP .
∴ ∠CPA= ∠CBP.
过P作PH⊥x轴于H.
∵ OC=OD=3,∠DOC=90°,
∴ ∠DCO=45°.∴ ∠PCH=45°
∴ PH=CH=CP![]() =4,
=4,
∴ H(-7,0),BH=12,
∴ P(-7,-4),
∴![]() ,
,
tan∠CPA=![]() .
.
(3) ∵ 抛物线的顶点是M(3,-4),
又 ∵ P(-7,-4),
∴ PM∥x轴 .
当点E在M左, 则∠BAM=∠AME.
∵ ∠AEM=∠AMB,
∴ △AEM∽△BMA.
∴![]() ,
,
∴![]() .
.
∴ ME=5,∴ E(-2,-4).
过点A作AN⊥PM于点N,则N(1,-4).
当点E在M右侧时,记为点![]() ,
,
∵ ∠A![]() N=∠AEN,
N=∠AEN,
∴ 点![]() 与E 关于直线AN对称,则
与E 关于直线AN对称,则![]() (4,-4).
(4,-4).
综上所述,E的坐标为(-2,-4)或(4,-4).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
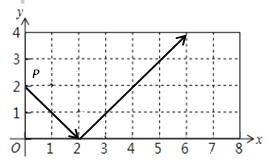
A.( 2,4 )B.( 2,0 )C.( 8,2)D.( 6,0 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取900°;而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
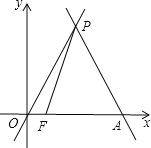
【题目】已知:如图,直线y=﹣![]() x+4
x+4![]() 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=![]() x交于点P.
x交于点P.
(1)求点P的坐标.
(2)动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.
(3)若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是菱形,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
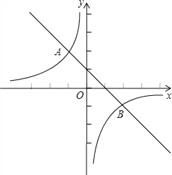
【题目】如图,已知一次函数y=kx+b与反比例函数![]() 的图象交于A(﹣1,m)、B(n,﹣1)两点.
的图象交于A(﹣1,m)、B(n,﹣1)两点.
(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解今年天河区九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分组(A:60分;B:59-54分;C:53-48分;D:47-36分;E:350分)统计如下:

根据上面提供的信息,回答下列问题:
(1)这次调查中,抽取的学生人数为多少?并将条形统计图补充完整;
(2)如果把成绩在48分以上(含48分)定为优秀,估计今年天河区9000名九年级学生中,体育成绩为优秀的学生人数有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com