
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯC1УлЕЧОпПЯC2УлxЦбУРПаН¬өДҪ»өгMЈ¬NЈЁөгMФЪөгNөДЧуІаЈ©Ј¬УлxЦбөДҪ»өг·ЦұрОӘAЈ¬BЈ¬ЗТөгAөДЧшұкОӘЈЁ0Ј¬©Ғ3Ј©Ј¬ЕЧОпПЯC2өДҪвОцКҪОӘyЈҪmx2+4mx©Ғ12mЈЁmЈҫ0Ј©Ј®
ЈЁ1Ј©ЗуMЈ¬NБҪөгөДЧшұкЈ»
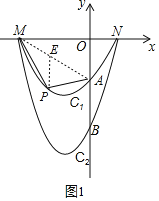
ЈЁ2Ј©ФЪөЪИэПуПЮДЪөДЕЧОпПЯC1ЙПКЗ·сҙжФЪТ»өгPЈ¬К№өГЎчPAMөДГж»эЧоҙуЈ¬ИфҙжФЪЈ¬ЗуіцЎчPAMөДГж»эөДЧоҙуЦөЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ»
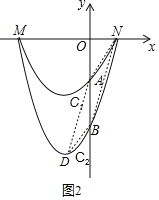
ЈЁ3Ј©ЙиЕЧОпПЯC2өД¶ҘөгОӘөгDЈ¬ЛіҙОБ¬ҪУAЈ¬DЈ¬BЈ¬NЈ¬ИфЛДұЯРОADBNКЗЖҪРРЛДұЯРОЈ¬ЗуmөДЦөЈ®
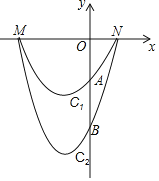
Ўҫҙр°ёЎҝЈЁ1Ј©MЈЁ©Ғ6Ј¬0Ј©Ј¬NЈЁ2Ј¬0Ј©Ј¬ЈЁ2Ј©aЈҪ©Ғ3КұЈ¬ЎчPAMөДГж»эЧоҙуЈ¬Гж»эөДЧоҙуЦөКЗ![]() Ј»ЈЁ3Ј©
Ј»ЈЁ3Ј©![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©БоyЈҪ0ҙъИлyЈҪmx2+4mx©Ғ12mЈ¬јҙҝЙЗуіцMЎўNБҪөгөДЧшұкЈ»
ЈЁ2Ј©АыУГөгAЎўMЎўNөДЧшұкјҙҝЙЗуіцЕЧОпПЯC1өДҪвОцКҪЈ¬ФЩЗуіцЦұПЯMAөДҪвОцКҪЈ¬И»әуЙиPөДәбЧшұкОӘaЈ¬№эөгPЧчPEЎОyЦбҪ»MAУЪөгEЈ¬ЛщТФЎчPAMөДГж»эОӘ![]() PEOMЈ¬БРіцЎчPAMөДГж»эУлaөДәҜКэ№ШПөКҪЈ¬АыУГ¶юҙОәҜКэөДРФЦКјҙҝЙЗуіцЎчPAMөДГж»эЧоҙуЦөЈ»
PEOMЈ¬БРіцЎчPAMөДГж»эУлaөДәҜКэ№ШПөКҪЈ¬АыУГ¶юҙОәҜКэөДРФЦКјҙҝЙЗуіцЎчPAMөДГж»эЧоҙуЦөЈ»
ЈЁ3Ј©өұANЎОDBКұЈ¬ЗуіцmөДЦөЈ¬ҙЛКұЦ»РиТӘЦӨГчANЈҪDBјҙҝЙЈ®
ҪвЈәЈЁ1Ј©БоyЈҪ0ҙъИлyЈҪmx2+4mx©Ғ12mЈ¬
Ўа0ЈҪmx2+4mx©Ғ12mЈ¬
ЎаxЈҪ2»тxЈҪ©Ғ6Ј¬
ЎаNЈЁ2Ј¬0Ј©Ј¬MЈЁ©Ғ6Ј¬0Ј©Ј»
ЈЁ2Ј©ЙиЕЧОпПЯC1өДҪвОцКҪОӘyЈҪaЈЁx©Ғ2Ј©ЈЁx+6Ј©Ј¬
°СCЈЁ0Ј¬©Ғ3Ј©ҙъИлyЈҪaЈЁx©Ғ2Ј©ЈЁx+6Ј©Ј¬
Ўа©Ғ3ЈҪ©Ғ12aЈ¬
Ўа![]() Ј¬
Ј¬
ЎаЕЧОпПЯөДҪвОцКҪОӘyЈҪ![]() Ј¬
Ј¬
ЙиЦұПЯAMөДҪвОцКҪОӘyЈҪkx+bЈ¬
°СMЈЁ©Ғ6Ј¬0Ј©әНAЈЁ0Ј¬©Ғ3Ј©ҙъИлyЈҪkx+bЈ¬
Ўа![]() Ј¬
Ј¬
Ўа Ј¬
Ј¬
ЎаЦұПЯAMөДҪвОцКҪОӘyЈҪ©Ғ![]() x©Ғ3Ј¬
x©Ғ3Ј¬
ЙиPөДЧшұкОӘЈЁaЈ¬![]() a2+a©Ғ3Ј©Ј¬ЖдЦР©Ғ6ЈјaЈј0Ј¬
a2+a©Ғ3Ј©Ј¬ЖдЦР©Ғ6ЈјaЈј0Ј¬
№эөгPЧчPEЎОyЦбҪ»MAУЪөгEЈ¬ИзНј1Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() ЈҪ
ЈҪ![]() Ј¬
Ј¬
Ўа![]() =
=![]() =
=![]() Ј¬
Ј¬
ЎаaЈҪ©Ғ3КұЈ¬ЎчPAMөДГж»эЧоҙуЈ¬Гж»эөДЧоҙуЦөКЗ![]() Ј®
Ј®
ЈЁ3Ј©ИзНј2Ј¬УЙЈЁ1Ј©ҝЙЦӘЈәNЈЁ2Ј¬0Ј©Ј¬AЈЁ0Ј¬©Ғ3Ј©Ј¬
ЎаУЙ№ҙ№Й¶ЁАнҝЙЦӘЈәANЈҪ![]() Ј¬
Ј¬
ЗуөГЦұПЯANөДҪвОцКҪОӘ![]() Ј¬
Ј¬
ЎаБоxЈҪ0ҙъИлyЈҪmx2+4mx©Ғ12mЈ¬
ЎаyЈҪ©Ғ12mЈ¬
ЎаBЈЁ0Ј¬©Ғ12mЈ©Ј¬
УЙЕЧОпПЯC2өДҪвОцКҪҝЙЦӘЈәDЈЁ©Ғ2Ј¬©Ғ16mЈ©Ј¬
ИфЛДұЯРОADBNКЗЖҪРРЛДұЯРОЈ¬
ЎаANЎОBDЈ¬
ЙиЦұПЯDBөДҪвОцКҪОӘ![]() Ј¬
Ј¬
Ўа©Ғ16mЈҪ©Ғ3©Ғ12mЈ¬
Ўа![]() Ј¬
Ј¬
ЎаBЈЁ0Ј¬9Ј©Ј¬DЈЁ©Ғ2Ј¬12Ј©Ј¬
Ўа![]() Ј¬
Ј¬
ЎаANЈҪBDЈ¬
Ўа![]() КұЈ¬ЛДұЯРОADBNКЗЖҪРРЛДұЯРОЈ®
КұЈ¬ЛДұЯРОADBNКЗЖҪРРЛДұЯРОЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
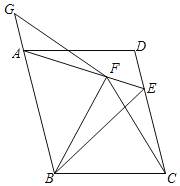
ЎҫМвДҝЎҝФЪЖҪРРЛДұЯРОABCDЦРЈ¬ТФABОӘұЯЧчөИұЯЎчABEЈ¬өгEФЪCDЙПЈ¬ТФBCОӘұЯЧчөИұЯЎчBCFЈ¬өгFФЪAEЙПЈ¬өгGФЪBAСУіӨПЯЙПЗТFGЈҪFBЈ®
ЈЁ1Ј©ИфCDЈҪ6Ј¬AFЈҪ3Ј¬ЗуЎчABFөДГж»эЈ»
ЈЁ2Ј©ЗуЦӨЈәBEЈҪAG+CEЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПCЈҪ90ЎгЈ¬ACЈҪ4![]() Ј¬BCЈҪ4Ј¬өгDКЗACөДЦРөгЈ¬өгFКЗұЯABЙПТ»¶ҜөгЈ¬СШDFЛщФЪЦұПЯ°СЎчADF·ӯХЫөҪЎчAЎдDFөДО»ЦГЈ¬ИфПЯ¶ОAЎдDҪ»ABУЪөгEЈ¬ЗТЎчBAЎдEОӘЦұҪЗИэҪЗРОЈ¬ФтBFөДіӨОӘ_____Ј®
Ј¬BCЈҪ4Ј¬өгDКЗACөДЦРөгЈ¬өгFКЗұЯABЙПТ»¶ҜөгЈ¬СШDFЛщФЪЦұПЯ°СЎчADF·ӯХЫөҪЎчAЎдDFөДО»ЦГЈ¬ИфПЯ¶ОAЎдDҪ»ABУЪөгEЈ¬ЗТЎчBAЎдEОӘЦұҪЗИэҪЗРОЈ¬ФтBFөДіӨОӘ_____Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
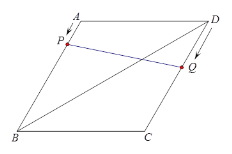
ЎҫМвДҝЎҝИзНјЈ¬ФЪБвРОABCDЦРЈ¬ТСЦӘЎПBADЈҪ120ЎгЈ¬¶ФҪЗПЯBDіӨОӘ12Ј®
ЈЁ1Ј©ЗуБвРОABCDөДЦЬіӨЈ»
ЈЁ2Ј©¶ҜөгPҙУөгAіц·ўЈ¬СШAЎъBөД·ҪПтЈ¬ТФГҝГл1ёцөҘО»өДЛЩ¶ИПтөгBФЛ¶ҜЈ»ФЪөгPіц·ўөДН¬КұЈ¬¶ҜөгQҙУөгDіц·ўЈ¬СШDЎъCЎъBөД·ҪПтЈ¬ТФГҝГл2ёцөҘО»өДЛЩ¶ИПтөгBФЛ¶ҜЈ®ЙиФЛ¶ҜКұјдОӘtЈЁsЈ©Ј®
ўЩөұPQЗЎәГұ»BDЖҪ·ЦКұЈ¬КФЗуtөДЦөЈ»
ўЪБ¬ҪУAQЈ¬КФЗуЈәФЪХыёцФЛ¶Ҝ№эіМЦРЈ¬өұtИЎФхСщөДЦөКұЈ¬ЎчAPQЗЎәГКЗТ»ёцЦұҪЗИэҪЗРОЈҝ

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
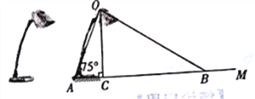
ЎҫМвДҝЎҝНјОӘ·ЕЦГФЪЛ®ЖҪЧАГжЙПөДМЁөЖөДЖҪГжКҫТвНјЈ¬ҝЙЙмЛхКҪөЖұЫAOіӨОӘ40 cm,УлЛ®ЖҪГжЛщРОіЙөДјРҪЗЎПOAMәгОӘ75Ўг(І»КЬөЖұЫЙмЛхөДУ°Пм).УЙ№вФҙ0ЙдіцөД№вПЯСШөЖХЦРОіЙ№вПЯOCЈ¬OBЈ¬УлЛ®ЖҪГжЛщРОіЙөДјРҪЗЎПOCA,ЎПOBA·ЦұрОӘ90ЎгәН30Ўг.
(1)ЗуёГМЁөЖХХББЧАГжөДҝн¶ИBC.(І»ҝјВЗЖдЛыТтЛШЈ¬Ҫб№ыҫ«И·өҪ1 cmЈ¬ІОҝјКэҫЭ:sin75ЎгЎЦ0.97,cos75ЎгЎЦ0.26Ј¬ ![]() ЎЦ1.73)
ЎЦ1.73)
(2)ИфөЖұЫЧо¶аҝЙЙміӨЦБ60 cm,І»өчХыөЖХЦөДҪЗ¶ИЈ¬ДЬ·сИГМЁөЖХХББЧАГж85 cmөДҝн¶И?
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
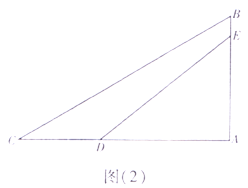
ЎҫМвДҝЎҝёЫЦй°ДҙуЗЕКЗЦР№ъҫіДЪТ»ЧщБ¬ҪУПгёЫЎўЦйәЈәН°ДГЕөДЗЕЛн№ӨіМЈ¬О»УЪЦР№ъ№г¶«КЎБжШкСуЗшУтДЪЈ¬ОӘЦйҪӯИэҪЗЦЮөШЗш»·ПЯёЯЛЩ№«В·ДП»·¶ОЈ¬ЗаЦЭәҪөАЗЕЎ°ЦР№ъҪбИэөШН¬РДЎұЦчМвөДРұАӯЛчЛюИзНјЈЁ1Ј©ЛщКҫ.ДіКэС§РЛИӨРЎЧйёщҫЭІДБПұаЦЖБЛИзПВКэС§ОКМвЈ¬ЗлДгҪвҙр.
ИзНјЈЁ2Ј©Ј¬BCЈ¬DEОӘЦчЛюABЈЁЦчЛюABУлЗЕГжACҙ№ЦұЈ©ЙПөДБҪМхёЦЛчЈ¬ЗЕГжЙПCЎўDБҪөгјдөДҫаАлОӘ16mЈ¬ЦчЛюЙПAЎўEБҪөгөДҫаАлОӘ18.4mЈ¬ТСЦӘBCУлЗЕГжACөДјРҪЗОӘ30ЎгЈ¬DEУлЗЕГжACөДјРҪЗОӘ38ЎгЎЈЗуЦчЛюABөДёЯ.ЈЁҪб№ыҫ«И·өҪ1ГЧЈ¬ІОҝјКэҫЭЈәsin38ЎгЎЦ0.6Ј¬cos38ЎгЎЦ0.8Ј¬tan38ЎгЎЦ0.8Ј¬![]() ЎЦ1.7Ј©
ЎЦ1.7Ј©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
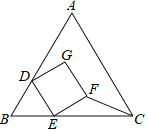
ЎҫМвДҝЎҝИзНјЈ¬өИұЯЎчABCУлХэ·ҪРОDEFGЦШөюЈ¬ЖдЦРDЎўEБҪөг·ЦұрФЪABЎўBCЙПЈ¬ЗТBDЈҪBEЈ¬ИфABЈҪ6Ј¬DEЈҪ2Ј¬ФтЎчEFCөДГж»эОӘ___Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ХэИэҪЗРОABCөДұЯіӨКЗ4Ј¬·ЦұрТФөгBЈ¬CОӘФІРДЈ¬ТФrОӘ°лҫ¶ЧчБҪМх»ЎЈ¬ЙиБҪ»ЎУлұЯBCО§іЙөДТхУ°Іҝ·ЦГж»эОӘSЈ¬өұ![]() ЎЬ
ЎЬ![]() Јј4КұЈ¬SөДИЎЦө·¶О§КЗ___Ј®
Јј4КұЈ¬SөДИЎЦө·¶О§КЗ___Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪ«ХэХыКэ°ҙИзНјЛщКҫөД№жВЙЕЕБРПВИҘЈ¬ИфУГУРРтКэ¶ФЈЁmЈ¬nЈ©ұнКҫөЪmЕЕЈ¬ҙУЧуөҪУТөЪnёцКэЈ¬ИзЈЁ3Ј¬2Ј©ұнКҫХэХыКэ5Ј¬ЈЁ4Ј¬3Ј©ұнКҫХэХыКэ9Ј¬ФтЈЁ20Ј¬19Ј©ұнКҫөДХэХыКэКЗ_____Ј®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com