
【题目】如图,正三角形ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当![]() ≤
≤![]() <4时,S的取值范围是___.
<4时,S的取值范围是___.

科目:初中数学 来源: 题型:
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
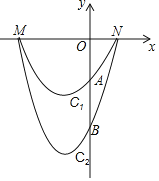
【题目】如图,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与x轴的交点分别为A,B,且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m(m>0).
(1)求M,N两点的坐标;
(2)在第三象限内的抛物线C1上是否存在一点P,使得△PAM的面积最大,若存在,求出△PAM的面积的最大值;若不存在,说明理由;
(3)设抛物线C2的顶点为点D,顺次连接A,D,B,N,若四边形ADBN是平行四边形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;
(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
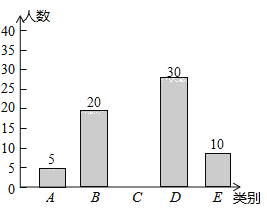
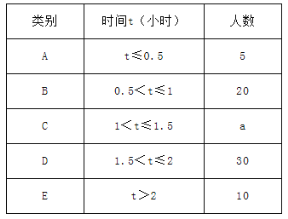
请根据图表信息解答下列问题:
(1)a=_____;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
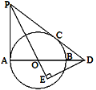
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=3,tan∠PDA=![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
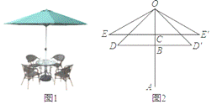
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见.如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠BOD=45°,当将遮阳伞撑开至OE位置时,测得∠BOE=60°,且此时遮阳伞边沿上升的竖直高度BC为30cm,求当遮阳伞撑开至OE位置时,伞下半径EC的长.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0; (2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1; (4)(x+3)2=(1﹣2x)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
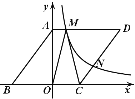
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com