
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
【答案】(1)甲、乙两种玩具分别是15元/件,25元/件;(2)故商场共有四种进货方案:方案一:购进甲种玩具20件,乙种玩具28件;方案二:购进甲种玩具21件,乙种玩具27件;方案三:购进甲种玩具22件,乙种玩具26件;方案四:购进甲种玩具23件,乙种玩具25件;(3)W=﹣5m+960,最大利润860元.
【解析】
(1)设甲种玩具进价为x元/件,则乙种玩具进价为(40﹣x)元/件,根据用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解;
(2)设购进甲种玩具m件,则购进乙种玩具(48﹣m)件,根据甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,可列出不等式组求解;
(3)先列出有关总利润和进货量的一次函数关系式,然后利用一次函数的性质结合自变量的取值范围求最大值即可.
(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
根据题意,得![]() ,
,
解得x=15,
经检验x=15是原方程的解,
则40﹣x=25,
答:甲、乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具m件,则购进乙种玩具(48﹣m)件,
由题意,得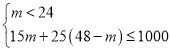 ,
,
解得20≤m<24,
∵m是整数,
∴m取20,21,22,23,
故商场共有四种进货方案:
方案一:购进甲种玩具20件,乙种玩具28件;
方案二:购进甲种玩具21件,乙种玩具27件;
方案三:购进甲种玩具22件,乙种玩具26件;
方案四:购进甲种玩具23件,乙种玩具25件;
(3)设购进甲种玩具m件,卖完这批玩具获利W元,则购进乙种玩具(48﹣m)件,
根据题意得:W=(30﹣15)m+(45﹣25)(48﹣m)=﹣5m+960,
∵比例系数k=﹣5<0,
∴W随着m的增大而减小,
∴当m=20时,有最大利润W=﹣5×20+960=860元.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

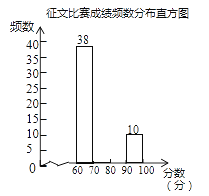
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探宄问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数n,我们进行如下操作:
(1)将n拆分为两个正整数m1,m2的和,并计算乘积m1×m2;
(2)对于正整数m1,m2,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即折分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,
请探究不同的拆分方式是否影响正整数n的“神秘值”,并说明理由.
(尝试探究):

(1)正整数1和2的“神秘值”分别是
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
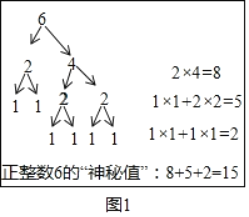
如图所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在如图中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在如图中绐出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数n的“神秘值”与其折分方法无关.请帮助小凯,利用尝试成果,猜想正整数n的“神秘值”的表达式为 ,(用含字母n的代数式表示,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
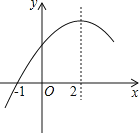
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵![]() ,即
,即![]() ,
,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() -2).
-2).
请解答:(1) ![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知: 10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(+11)+(﹣12)﹣(+18)
(2)2.25+(+0.75)﹣(+2![]() )+(﹣1.75)
)+(﹣1.75)
(3)﹣17÷![]() ×(﹣9)
×(﹣9)
(4)(﹣3)2﹣[(﹣12)×(﹣![]() )+(﹣2)3]
)+(﹣2)3]
查看答案和解析>>
科目:初中数学 来源: 题型:
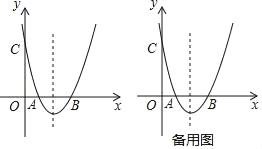
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线y=x2+bx+c的表达式;
(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com