
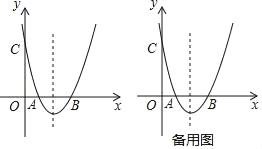
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线y=x2+bx+c的表达式;
(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
【答案】(1)y=x2﹣4x+3;(2)(2,﹣1);(3)![]() .
.
【解析】试题分析:(1)利用待定系数法求抛物线解析式;
(2)如图1,设D(2,y),利用两点间的距离公式得到BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,然后讨论:当BD为斜边时得到18+4+(y﹣3)2=1+y2;当CD为斜边时得到4+(y﹣3)2=1+y2+18,再分别解方程即可得到对应D的坐标;
(3)先证明∠CEF=90°得到△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,则PE=![]() PG,PF=
PG,PF=![]() PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣
PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣![]() t2+4
t2+4![]() t,然后利用二次函数的性质解决问题.
t,然后利用二次函数的性质解决问题.
试题解析:解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得: ![]() ,解得:
,解得: ![]() ,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;
,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;
(2)如图1,抛物线的对称轴为直线x=﹣![]() =2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);
=2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);
当△BCD是以BC为直角边,CD为斜边的直角三角形时,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得:y=﹣1,此时D点坐标为(2,﹣1);
(3)易得BC的解析式为y=﹣x+3.∵直线y=x+m与直线y=x平行,∴直线y=﹣x+3与直线y=x+m垂直,∴∠CEF=90°,∴△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,PE=![]() PG,PF=
PG,PF=![]() PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=
PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=![]() PH=
PH=![]() t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=
t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=![]() PG=﹣
PG=﹣![]() t2+
t2+![]() t,∴PE+EF=PE+PE+PF=2PE+PF=﹣
t,∴PE+EF=PE+PE+PF=2PE+PF=﹣![]() t2+3
t2+3![]() t+
t+![]() t=﹣
t=﹣![]() t2+4
t2+4![]() t=﹣
t=﹣![]() (t﹣2)2+4
(t﹣2)2+4![]() ,当t=2时,PE+EF的最大值为4
,当t=2时,PE+EF的最大值为4![]() .
.


科目:初中数学 来源: 题型:
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探究问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数![]() ,我们进行如下操作:
,我们进行如下操作:
(1)将![]() 拆分为两个正整数
拆分为两个正整数![]() ,
,![]() 的和,并计算乘积
的和,并计算乘积![]() ;
;
(2)对于正整数![]() ,
,![]() ,分别重复此操作,得到另外两个乘积;
,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即拆分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,请探究不同的拆分方式是否影响正整数![]() 的“神秘值”,并说明理由.
的“神秘值”,并说明理由.
(尝试探究):
(1)正整数2的“神秘值”是_________;
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
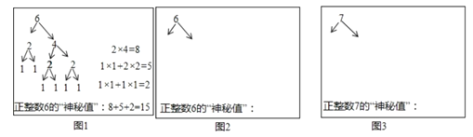
如图1所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在图2中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在图3中给出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数![]() 的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数
的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数![]() 的“神秘值”的表达式为________.(用含字母
的“神秘值”的表达式为________.(用含字母![]() 的代数式表示,直接写出结果)
的代数式表示,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
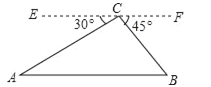
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 75 | 75 | ||
乙 | 33.3 | 70 |
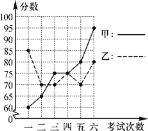
(1)请根据统计图填写上表:
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看,你得出什么结论;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
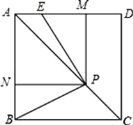
【题目】如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN;
(3)若点P在线段AC上移动,其他不变,设PC=x,AE=y,求y关于x的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
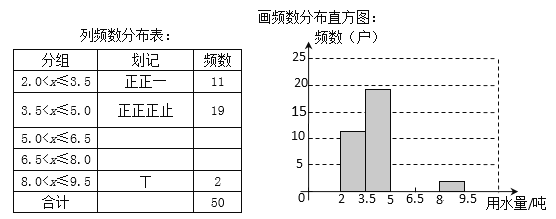
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com