
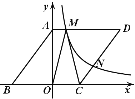
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)先根据菱形的性质求出AD=AB=5,再根据三角函数求出OA,进而利用勾股定理求出OB,求出点C,D坐标,利用待定系数法求出直线CD解析式,进而求出点N坐标,最后用待定系数法即可得出结论;
(2)先求出点M坐标,再用两点间的距离公式求出OM和CM,即可得出结论.
:(1)∵四边形ABCD是菱形,
∴AD∥BC,AB=AD=BC=5,
在Rt△AOB中,sin∠ABC=![]() ,
,
∴OA=4,
根据勾股定理得,OB=3,
∴OC=BC-OB=2,
∴C(2,0),
∵AD=5,OA=4,
∴D(5,4),
∴直线CD的解析式为y=![]() x-
x-![]() ,
,
∵点N的坐标是(3,n),
∴n=![]() ,
,
∴N(3,![]() ),
),
∵点N在反比例函数y=![]() (x>0)图形上,
(x>0)图形上,
∴k=3×![]() =4,
=4,
∴反比例函数的解析式为y=![]() ;
;
(2)由(1)知,反比例函数的解析式为y=![]() ,
,
∵点M在AD上,
∴M点的纵坐标为4,
∴点M的横坐标为1,
∴M(1,4),
∵C(2,0),
∴OM=![]() ,CM=
,CM=![]() ,
,
∴OM=CM,
∴△OMC是等腰三角形.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,点
,点![]() 是
是![]() 上一点,当点
上一点,当点![]() 到点
到点![]() 和点
和点![]() 的距离相等时,求
的距离相等时,求![]() 的长;
的长;
(2)若![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
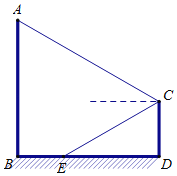
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的![]() ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
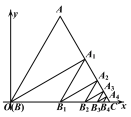
【题目】如图,等边三角形ABC的边长为1,顶点B与原点O重合,点C在x轴的正半轴上,过点B作BA1⊥AC于点A1,过点A1作A1B1∥OA,交OC于点B1;过点B1作B1A2⊥AC于点A2,过点A2作A2B2∥OA,交OC于点B2;……,按此规律进行下去,点A2020的坐标是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
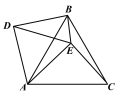
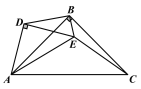
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE=![]() ,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
(1)如图1,当![]() =60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
=60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
(2)如图2当![]() =90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
=90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若BC=![]() ,请直接写出△BDE的面积.
,请直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
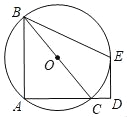
【题目】如图,已知△ABC内接于⊙O,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接BE.DE=12,
(1)若CD=4,求⊙O的半径;
(2)若AD+CD=30,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
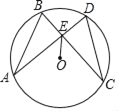
【题目】如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
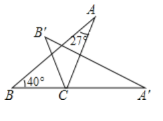
【题目】如图,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() ,使点
,使点![]() 落在
落在![]() 的延长线上.已知
的延长线上.已知![]() ,则
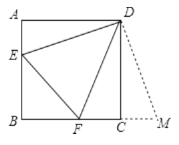
,则![]() ___________度;如图,已知正方形
___________度;如图,已知正方形![]() 的边长为
的边长为![]() 分别是
分别是![]() 边上的点,且
边上的点,且![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .若
.若![]() ,则
,则![]() 的长为_________ .
的长为_________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com