
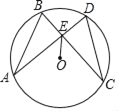
【题目】如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
【答案】(1)证明见解析;(2)AE=7.
【解析】
(1)欲证明AB=CD,只需证得![]() .
.
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
(1)证明:如图,∵AD=BC,
∴![]() =
= ![]() ,
,
∴![]() ﹣
﹣ ![]() =
=![]() ﹣
﹣![]() ,即
,即![]() =
=![]() ,
,
∴AB=CD;
(2)如图,过 O 作 OF⊥AD 于点 F,作 OG⊥BC 于点 G,连接 OA、OC.
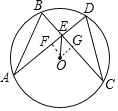
则 AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在 Rt△AOF 与 Rt△COG 中,![]() ,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形 OFEG 是正方形,
∴OF=EF.
设 OF=EF=x,则 AF=FD=x+1,
在直角△OAF 中.由勾股定理得到:x2+(x+1)2=52, 解得 x=5.
则 AF=3+1=4,即 AE=AF+3=7.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,1),B(-1,3),C(0,1).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(-5,-3),画出平移后的△A2B2C2;
(3)若△A2B2C2和△A1B1C关于点P中心对称,请直接写出旋转中心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
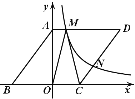
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
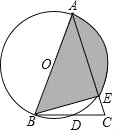
【题目】如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是弧BE的中点,
(1)求证AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积;
(3)当∠A为锐角时,试说明∠A与∠CBE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
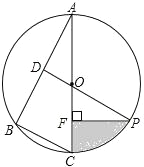
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
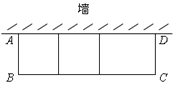
【题目】如图,用一段100米长的篱笆围成一个一边靠墙(墙足够长),中间用篱笆隔开的矩形养殖场,中间用两道篱笆隔开分出三个小的矩形,设矩形垂直于墙的一边长为x 米,矩形ABCD的面积记为y平方米.
(1)直接写出y与x的函数关系式及自变量x的取值范围;
(2)当x=8,求y的值;
(3)当x取何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )

A. (1)(2)(3)(4) B. (2)(4)(5) C. (2)(3)(4) D. (1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )

A. (80+2x)(50+2x)=5400 B. (80-x)(50-x)=5400
C. (80+x)(50+x)=5400 D. (80-2x)(50-2x)=5400
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com