
【题目】如图,![]() 的对角线
的对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,成立的个数有( )
,成立的个数有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
由ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=![]() BC,证得∠CAD=30°;继而证得AC⊥AB,AE=CE,可判断①;由AC⊥AB,则②SABCD=ABAC;可得OE是三角形的中位线,则OE=
BC,证得∠CAD=30°;继而证得AC⊥AB,AE=CE,可判断①;由AC⊥AB,则②SABCD=ABAC;可得OE是三角形的中位线,则OE=![]() AB,则③
AB,则③![]() ;证得④
;证得④![]() .
.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,∠BAE=60°,
∵AB=![]() BC,
BC,
∴AE=![]() BC,
BC,
∴∠BAC=90°,
∴∠ACE=∠CAE=30°,
∴AE=CE,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵点O是AC中点,点E是BC中点,
∴OE=![]() AB,
AB,
∴![]() ,故③错误;
,故③错误;
∵OE是中位线,
∴OE=![]() AB=
AB=![]() BC,故④正确.
BC,故④正确.
∴正确的选项有①②④,共3个;
故选:C.


科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
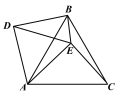
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE=![]() ,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
(1)如图1,当![]() =60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
=60°时,线段BD与CE的数量关系为 ,线段EA,EB,EC的数量关系为 ;
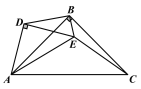
(2)如图2当![]() =90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
=90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若BC=![]() ,请直接写出△BDE的面积.
,请直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发, 到达目的地后停止,设慢车行驶时间为 x 小时,两车之间的距离为 y 千米,两者的关系如图 所示:
(1)两车出发 小时后相遇;
(2)求快车和慢车的速度;
(3)求线段 BC 所表示的 y 与 x 的 关系式,并求两车相距 300 千米时的时间.
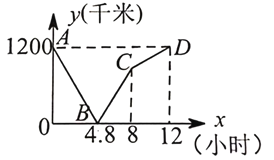
查看答案和解析>>
科目:初中数学 来源: 题型:
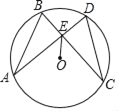
【题目】如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(3,a)(其中a>4),射线OA与反比例函数y=![]() 的图象交于点P,点B、C分别在函数y=
的图象交于点P,点B、C分别在函数y=![]() 的图象上,且AB∥x轴,AC∥y轴;
的图象上,且AB∥x轴,AC∥y轴;
(1)当点P横坐标为2,求直线AO的表达式;
(2)连接CO,当AC=CO时,求点A坐标;
(3)连接BP、CP,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
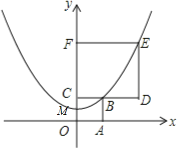
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com