
【题目】如图已知![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,点
,点![]() 是
是![]() 上一点,当点
上一点,当点![]() 到点
到点![]() 和点
和点![]() 的距离相等时,求
的距离相等时,求![]() 的长;
的长;
(2)若![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)如图1中,连接AB,作线段AB的中垂线MN,交AB于N,交EF于M,连接AM,BM.设DM=x.根据MA=MB构建方程即可解决问题;
(2)如图2中,如图,作点A故直线GH 的对称点A′,点B关于直线EF的对称点B′,连接A′B′交GH于点P,交EF于点Q,作B′H⊥CA交CA的延长线于H.则此时AP+PQ+QB的值最小.最小值为线段A′B′的长;
解:(1)如图1中,连接AB,作线段AB的中垂线MN,交AB于N,交EF于M,连接AM,BM.设DM=x.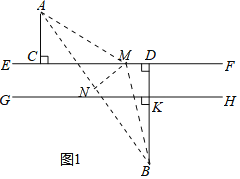
在Rt△ACM中,AM2=AC2+CM2=32+(6-x)2,
在Rt△BDM中,BM2=DM2+BD2=x2+62,
∵AM=MB,
∴32+(6-x)2=x2+62,
解得x=![]() ,
,
∴CM=CD-MD=6- ![]() =
= ![]() .
.
(2)如图2中,如图,作点A故直线GH 的对称点A′,点B关于直线EF的对称点B′,连接A′B′交GH于点P,交EF于点Q,作B′H⊥CA交CA的延长线于H.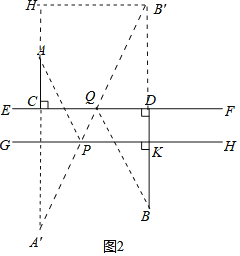
则此时AP+PQ+QB的值最小.
根据对称的性质可知:PA=PA′,QB=QB′,
∴PA+PQ+QB=PA′+PQ+QB′=A′B′,
∴PA+PQ+PB的最小值为线段A′B′的长,
在Rt△A′B′H中,∵HB′=CD= ![]() ,
,
HA′=DB′+CA′=7+6=13,
∴A′B′= 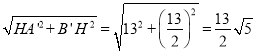 ,
,
∴AP+PQ+QB的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
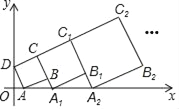
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )

A. (![]() ,0)B. (
,0)B. (![]() ,0)C. (
,0)C. (![]() ,0)D. (
,0)D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
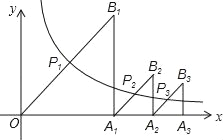
【题目】如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An﹣1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An﹣1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数![]() 的图象上,则y1+y2+y3+…+yn=_____.
的图象上,则y1+y2+y3+…+yn=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
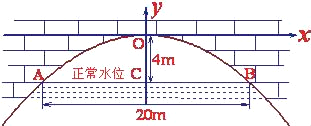
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式;
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,1),B(-1,3),C(0,1).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(-5,-3),画出平移后的△A2B2C2;
(3)若△A2B2C2和△A1B1C关于点P中心对称,请直接写出旋转中心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
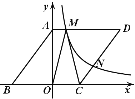
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com