
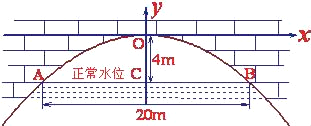
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式;
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
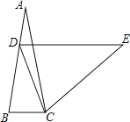
A. 80° B. 70° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
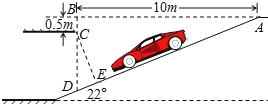
【题目】如图是菏泽银座地下停车场入口的设计图,请根据图中数据计算 CE的长度.(结果精确到 0.01m,参考数据:sin22°≈0.3746,cos22°≈0.9272, tan22°≈0.4040)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,点
,点![]() 是
是![]() 上一点,当点
上一点,当点![]() 到点
到点![]() 和点
和点![]() 的距离相等时,求
的距离相等时,求![]() 的长;
的长;
(2)若![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
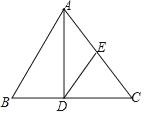
【题目】已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=21,AD=8,sinB=![]() .
.
求:(1)线段DC的长;
(2)tan∠EDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得到△EDC,当点B的对应点D恰好落在AC边上时,∠CAE的度数为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
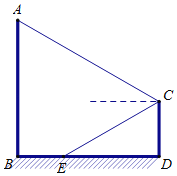
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
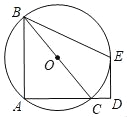
【题目】如图,已知△ABC内接于⊙O,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接BE.DE=12,
(1)若CD=4,求⊙O的半径;
(2)若AD+CD=30,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com