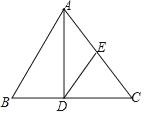
【题目】已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC=21，AD=8，sinB=
．
求：（1）线段DC的长；
（2）tan∠EDC的值．
【答案】（1）15；（2）
【解析】
第（1）问中要求CD的长，已知条件中给出了BC的长，这时只要求出BD的长即可；
利用三角函数的定义和AD的长可以得到AB的长，再在Rt△ABD中利用勾股定理得到BD的长，继而求出CD的长；
第（2）问是求一个锐角的正切值，需要放在直角三角形中求解，因此，要求tan∠CDE的值，就需将∠CDE进行转化；
利用直角三角形斜边上的中线可以得到DE=EC，进而得到∠EDC=∠ECD，从而将问题转化为求∠EDC的正切值.
解：（1）∵AD是BC边上的高，△ABD和△ACD是直角三角形，
在Rt△ABD中，∵sinB=
，AD=8，
∴
=，
∴AB=10，
∴BD=
=6，
又∵BC=21，
∴CD=BC﹣BD=15；
（2）在Rt△ACD中，
∵E为斜边AC的中点，
∴ED=EC=
AC，
∴∠C=∠EDC，
∴tan∠EDC=tanC=
=
．
科目：初中数学 来源： 题型：
【题目】已知O为坐标原点，A，B分别在y轴、x轴正半轴上，D是x轴正半轴上一动点，AD＝DE，∠ADE＝α，矩形AOBC的面积为32且AC＝2BC．
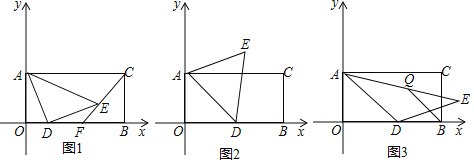
（1）如图1，当α＝90°时，直线CE交x轴于点F，求证：F为OB中点；
（2）如图2，当α＝60°时，若D是OB中点，求E点坐标；
（3）如图3，当α＝120°时，Q是AE的中点，求D点运动过程中BQ的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
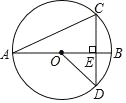
【题目】如图，线段 AB 是⊙O 的直径，弦 CD⊥AB，AB=8，∠CAB=22.5°，则 CD的长等于___________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y＝
(k≠0)在第一象限的图象经过顶点A(m，2)和CD边上的点E(n，
)，过点E的直线l交x轴于点F，交y轴于点G(0，－2)，则点F的坐标是( )
A. (
，0)B. (
，0)C. (
，0)D. (
，0)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】重庆八中渝北校区前的同茂大道
的路有一座小山
，因工程开发需要爆破．小山北偏东
方向，距小山
米的
处是同茂大道中央公园东公交站；小山北偏西
方向，距小山
米的
处是同茂大道上麗山公交站．
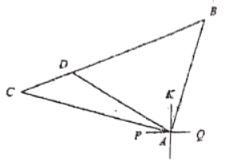
（1）爆破时，在爆破点周围
米范围有危险请问，为了安全，在爆破小山时需不需要暂时封闭同茂大道？请通过计算说明理由；
（2）点
是同茂大道上一点（点不与点重合），
，
区域是规划中的公园，问：这个公园占地多少平方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
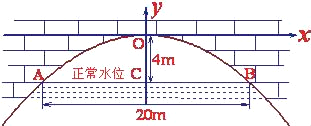
【题目】有一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m．
（1）在如图所示的直角坐标系中，求出该抛物线的解析式；
（2）设正常水位时桥下的水深为2m，为保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水深超过多少米时就会影响过往船只在桥下的顺利航行．
查看答案和解析>>
科目：初中数学 来源： 题型：
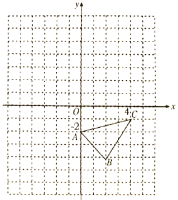
【题目】如图，在平面直角坐标系
中，
，
，
．
（1）请画出
关于
轴对称的
（其中
，
，
分别是
，
，
的对称点，不写画法，写出、、的坐标）
（2）在
轴上是否存在一点
，使
的值最小，若有，请作出点，并直接写出点的坐标，若没有，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于
的方程：
．
（1）如果此方程只有一个实数根，求
的值；
（2）如果此方程有两个实数根，求的取值范围；
（3）如果此方程无实数根，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
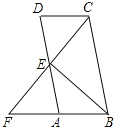
【题目】如图，在平行四边形ABCD中，点E为AD的中点，延长CE交BA的延长线于点F．
（1）求证：AB＝AF；
（2）若BC＝2AB，∠BCD＝100°，求∠ABE的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com