
【题目】重庆八中渝北校区前的同茂大道![]() 的路有一座小山
的路有一座小山![]() ,因工程开发需要爆破.小山
,因工程开发需要爆破.小山![]() 北偏东
北偏东![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 处是同茂大道中央公园东公交站;小山北偏西
处是同茂大道中央公园东公交站;小山北偏西![]() 方向,距小山
方向,距小山![]() 米的
米的![]() 处是同茂大道上麗山公交站.
处是同茂大道上麗山公交站.
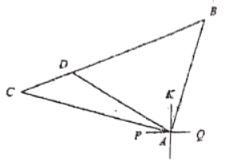
(1)爆破时,在爆破点![]() 周围
周围![]() 米范围有危险请问,为了安全,在爆破小山时需不需要暂时封闭同茂大道
米范围有危险请问,为了安全,在爆破小山时需不需要暂时封闭同茂大道![]() ?请通过计算说明理由;
?请通过计算说明理由;
(2)点![]() 是同茂大道
是同茂大道![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 区域是规划中的公园,问:这个公园占地多少平方米?
区域是规划中的公园,问:这个公园占地多少平方米?
【答案】(1)见解析;(2)67200平方米.
【解析】
(1)由题意得到∠CAK=74°,∠BAK=16°,AB=600,AC=800,求得∠CAB=90°,BC=![]() =1000米,过A作AH⊥BC于H,根据三角形的面积列方程即可得到结论;
=1000米,过A作AH⊥BC于H,根据三角形的面积列方程即可得到结论;
(2)根据勾股定理得到BH=![]() =360,根据三角形的面积公式即可得到结论.
=360,根据三角形的面积公式即可得到结论.
解:(1)在爆破小山时需不需要暂时封闭同茂大道BC;
理由:由题意得,∠CAK=74°,∠BAK=16°,AB=600,AC=800,
∴∠CAB=90°,BC=![]() =1000米,
=1000米,
过A作AH⊥BC于H,
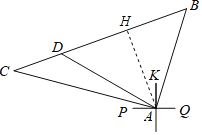
∴S△ABC=![]() BCAH=
BCAH=![]() ACAB,
ACAB,
∴AH=![]() =480米>400米,
=480米>400米,
∴在爆破小山时需不需要暂时封闭同茂大道BC;
(2)∵AD=AB,AH⊥BD,
∴BH=![]() =360,
=360,
∴CD=1000-2×360=280,
∴S△ACD=![]() ×280×480=67200m2,
×280×480=67200m2,
答:这个公园占地67200平方米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
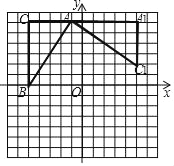
【题目】如图,△A1AC1是由△ABC绕某点P按顺时针方向旋转90°得到的,△ABC的顶点坐标分A(﹣1,6),B(﹣5,0),C(﹣5,6).
(1)求旋转中心P和点A1,C1的坐标;
(2)在所给网格中画出△A1AC1绕点P按顺时针方向旋转90°得到的图形;
(3)在所给网格中画出与△A1AC1关于点P成中心对称的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
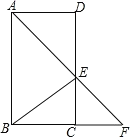
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
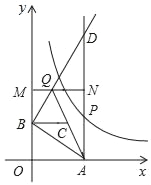
【题目】如图所示,已知:![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2![]() ,此时P点的坐标为( )
,此时P点的坐标为( )
A. (3,2) B. (![]() ,3
,3![]() ) C. (
) C. (![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
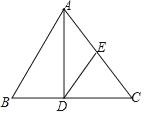
【题目】已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=21,AD=8,sinB=![]() .
.
求:(1)线段DC的长;
(2)tan∠EDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店的某种毛笔每支售价25元,书法练习本每本售价5元,该商店为促销正在进行优惠活动:
活动1:买一支毛笔送一本书法练习本;
活动2:按购买金额的九折付款.
某学校准备为书法兴趣小组购买这种毛笔20支,书法练习本x(x≥20)本.
(1)写出两种优惠活动实际付款金额y1(元),y2(元)与x(本)之间的函数关系式;
(2)请问:该校选择哪种优惠活动更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
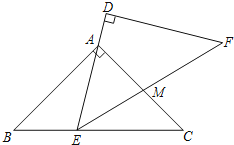
【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=![]() .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com