
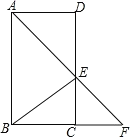
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)因为四边形![]() 是平行四边形,所以根据条件证明
是平行四边形,所以根据条件证明![]() 即可;(2)过点B作
即可;(2)过点B作![]() 于点H,在Rt△BCE中,由勾股定理求出
于点H,在Rt△BCE中,由勾股定理求出![]() ,在Rt△AHB中,求出
,在Rt△AHB中,求出![]() ,然后根据定义可求sin∠AEB的值.
,然后根据定义可求sin∠AEB的值.
试题解析:(1)证明:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() //BC.
//BC.
![]() ∠DAF=∠F.
∠DAF=∠F.
![]() ∠F=45°,
∠F=45°,
![]() ∠DAE=45°. 1分
∠DAE=45°. 1分
![]() AF是∠BAD的平分线,
AF是∠BAD的平分线,
![]() .
.
![]() .
.
又![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形ABCD是矩形. 2分
四边形ABCD是矩形. 2分
(2)解:过点B作![]() 于点H,如图.
于点H,如图.
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,
![]() AB=CD,AD=BC,∠DCB=∠D=90°.
AB=CD,AD=BC,∠DCB=∠D=90°.
![]() AB=14,DE=8,
AB=14,DE=8,
![]() CE=6.
CE=6.
在Rt△ADE中,∠DAE=45°,
![]() ∠DEA=∠DAE=45°.
∠DEA=∠DAE=45°.
![]() AD=
AD=![]() =8.
=8.
![]() BC=8.
BC=8.
在Rt△BCE中,由勾股定理得
![]() . 3分
. 3分
在Rt△AHB中,∠HAB=45°,
![]()
![]() . 4分
. 4分
![]() 在Rt△BHE中,∠BHE=90°,
在Rt△BHE中,∠BHE=90°,
![]() sin∠AEB=
sin∠AEB=![]() . 5分
. 5分


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
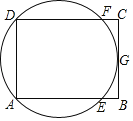
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
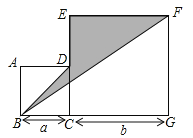
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式
化为分数形式
由于![]() =0.777…,设x=0.777…①
=0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x=![]() ,于是得
,于是得![]() =
=![]() .
.
同理可得![]() =
=![]() ,
,![]() =1+
=1+![]() =1+
=1+![]() ,
,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1)![]() = ,
= ,![]() = ;
= ;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(能力提升)
(3)![]() = ,
= ,![]() = ;
= ;
(注:![]() =0.315315…,
=0.315315…,![]() =2.01818…)
=2.01818…)
(探索发现)
(4)①试比较![]() 与1的大小:
与1的大小:![]() 1(填“>”、“<”或“=”)
1(填“>”、“<”或“=”)
②若已知![]() =
=![]() ,则
,则![]() = .
= .
(注:![]() =0.285714285714…)
=0.285714285714…)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为线段MN的中点,直线PQ与MN相交于点O,利用此图:
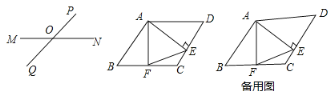
(1)作一个平行四边形AMBN,使A、B两点都在直线PQ上(只保留作图痕迹,不写作法)
(2)根据上述经验探究:在□ ABCD中,AE上CD交CD于E点,F为BC的中点,连接EF、AF,试猜想EF与AF的数里关系,并给予证明.
(3)若∠D=60°,AD=4,CD=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在前面的学习中,我们通过对同一面积的不同表达和比较,根据图①和图②发现并验证了平方差公式和完全平方公式.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.
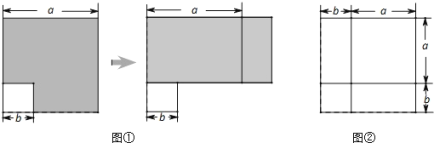
请你利用上述方法解决下列问题:
(1)请写出图1和图2所表示的代数恒等式
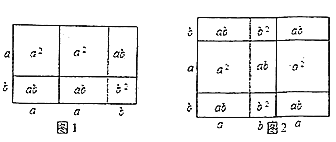
_______ _______
(2)现有a×a,b×b的正方形纸片和a×b的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次,每两个纸片之间既不重叠,也无空隙,拼出的图形中必须保留拼图的痕迹),使拼出的矩形面积为为2a2+5ab+2b2,并标出此矩形的长和宽.
(拓展应用)
提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:用矩形的面积表示两个正数的乘积,以47×43为例:
(1)画长为47,宽为43的矩形,如图③,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面.
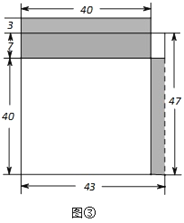
(2)原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,47×43=(40+10)×40+3×7=5×4×100+3×7=2021,
用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述)_________.
证明上述速算方法的正确性;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,点
表示的数为-10,点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 距离的3倍,点
距离的3倍,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)数轴上点![]() 对应的数是______.
对应的数是______.
(2)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com