
【题目】如图,点O为线段MN的中点,直线PQ与MN相交于点O,利用此图:
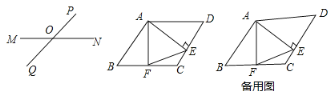
(1)作一个平行四边形AMBN,使A、B两点都在直线PQ上(只保留作图痕迹,不写作法)
(2)根据上述经验探究:在□ ABCD中,AE上CD交CD于E点,F为BC的中点,连接EF、AF,试猜想EF与AF的数里关系,并给予证明.
(3)若∠D=60°,AD=4,CD=3,求EF的长.
【答案】(1)见解析;(2) EF=AF,理由见解析;(3)![]()
【解析】
(1)利用平行四边形的判定即可作出图形;
(2)先判断出△ABF≌△GCF,得出AF=GF,进而判断出四边形ABGC为平行四边形,最后用直角三角形斜边的中线等于斜边的一半即可;
(3)先根据勾股定理求出AE,再由平行四边形的性质得出GE,最后勾股定理求出AG,最后用直角三角形的性质即可.
(1)如图1所示,四边形AMBN是所求作的平行四边形,
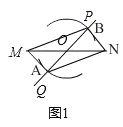
(2)结论:EF=AF,
理由:如图2,延长AF交DC的延长线于点G,连接BG,AC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠CGF,
∵点F是BC的中点,
∴BF=CF,
在△ABF和△GCF中,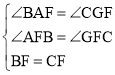 ,
,
∴△ABF≌△GCF,
∴AF=GF,
∵BF=CF,
∴四边形ABGC为平行四边形,
∴AF=GF,
∵AE⊥DC,
在Rt△AEG中,EF是斜边AG上的中线,
∴EF=AF=![]() AG;
AG;
(3)在Rt△AED中,∠D=60°,AD=4,
∴DE=![]() AD=2,由勾股定理得,AE=
AD=2,由勾股定理得,AE=![]() ,
,
由(2)知,在平行四边形ABGC中,CG=AB=CD=3,
∴GE=CG+CE=4,
在Rt△AEG中,AG=![]() ,
,
∴EF=![]() .
.



 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
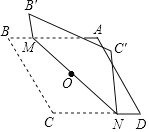
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
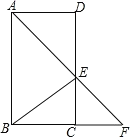
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.

(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
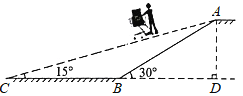
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,并比小明早到达,已知爸爸的平均速度是小明从家到中心书城平均速度的两倍.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
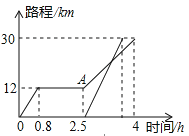
(1)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(2)小明从中心书城到滨海公园的平均速度是 km/h,
(3)小明爸爸比小明早到达多长时间?
(4)爸爸驾车经过多长时间追上小明?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.

据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生,m的值是 .
(2)请根据据以上信息直在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝国庆节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校分别单独购买服装,一共应付5000元.
(1)甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com