
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
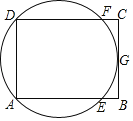
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】连接DG、AG,作GH⊥AD于H,连接OD,如图,先确定AG=DG,则GH垂直平分AD,则可判断点O在HG上,再根据HG⊥BC可判定BC与圆O相切;接着利用OG=OD可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心.
连接DG、AG,作GH⊥AD于H,连接OD,如图,
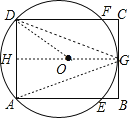
∵G是BC的中点,
∴AG=DG,
∴GH垂直平分AD,
∴点O在HG上,
∵AD∥BC,
∴HG⊥BC,
∴BC与圆O相切;
∵OG=OD,
∴点O不是HG的中点,
∴圆心O不是AC与BD的交点;
而四边形AEFD为⊙O的内接矩形,
∴AF与DE的交点是圆O的圆心;
∴(1)错误,(2)(3)正确.
故选:C.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
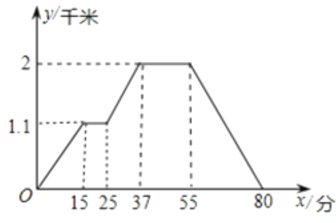
【题目】如图,反映的过程是小涛从家出发,去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小涛离家的距离.
(1)菜地离小涛家的距离是________km,小涛走到菜地用了_______min,小涛给菜地浇水用了_______min;
(2)小涛从菜地到玉米地用了____min,小涛给玉米地锄草用了________ min;
(3)玉米地离小涛家的距离是________km,小涛从玉米地走回家的平均速度是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
第一行:![]() ···
···
第二行:![]() ···
···
第三行 :![]() ···
···
探索它们之间的关系,寻求规律解答下列问题:
![]() 直接写出第②行数的第
直接写出第②行数的第![]() 个数是_____ ;
个数是_____ ;
![]() 直接写出第二行第
直接写出第二行第![]() 个数是 ,第三行第
个数是 ,第三行第![]() 个数是
个数是
![]() 取每行的第
取每行的第![]() 个数,请判断是否存在这样的
个数,请判断是否存在这样的![]() 个数使它们的和为
个数使它们的和为![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,DE∥AB分别交BC、AC于点D、E,过点E做EF⊥DE,交线段BC的延长线于点F。
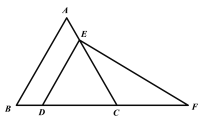
(1)求证:CE=CF;
(2)若BD=![]() CE,AB=8,求线段DF的长。
CE,AB=8,求线段DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
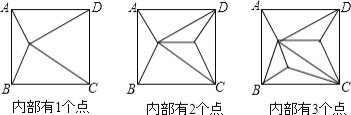
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
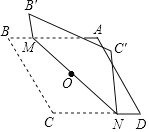
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏天容易发生腹泻等肠道疾病。益阳市医药公司的甲、乙两仓库内分别存有医治腹泻的药品80箱和70箱.现需要将库存的药品凋往南县100箱和沅江50箱,已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示:

(1)设从甲仓库运送到南县的药品为x箱,求总费用y(元)与x(箱)之间的函数关系式.并写出x的取值范围;
(2)求出最低费用,并说明总费用最低时的调配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
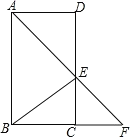
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com