练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知，两点在数轴上，点表示的数为－10，点到点的距离是点到点距离的3倍，点以每秒3个单位长度的速度从点向右运动.点以每秒2个单位长度的速度从点向右运动（点、同时出发）

    （1）数轴上点对应的数是______.

    （2）经过几秒，点、点分别到原点的距离相等.

    【答案】（1）30（2）秒或秒

    【解析】

    （1）根据点A表示的数为-10，OB=3OA，可得点B对应的数；

    （2）分①点M、点N在点O两侧；②点M、点N重合两种情况讨论求解；

    （1）∵OB=3OA=30．故B对应的数是30；（2）设经过x秒，点M、点N分别到原点O的距离相等；

    ①点M、点N在点O两侧，则10-3x=2x，解得x=2；②点M、点N重合，则3x-10=2x，解得x=10．

    所以经过2秒或10秒，点M、点N分别到原点O的距离相等.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

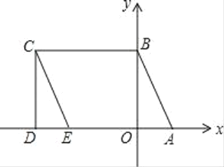
    【题目】如图所示，A（1，0）、点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为（-3，2）．

    （1）直接写出点E的坐标　 　；D的坐标 　 　

    （3）点P是线段CE上一动点，设∠CBP=x°，∠PAD=y°，∠BPA=z°，确定x， y，z之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB∥CD，点M，N分别是AB，CD上两点，点G在AB，CD之间．

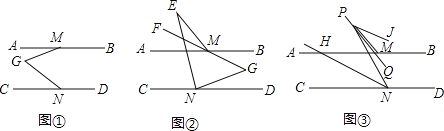
    （1）求证：∠AMG+∠CNG＝∠MGN；

    （2）如图②，点E是AB上方一点，MF平分∠AME，若点G恰好在MF的反向延长线上，且NE平分∠CNG，2∠E+∠G＝90°，求∠AME的度数；

    （3）如图③，若点P是（2）中的EM上一动点，PQ平分∠MPQ．NH平分∠PNC，交AB于点H，PJ∥NH，直接写出∠JPQ的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九（1）班同学为了解 2011 年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理．请解答以下问题：

    (1) 把上面的频数分布表和频数分布直方图补充完整；

    (2) 求月均用水量不超过 的家庭数占被调查家庭总数的百分比；

    (3) 若该小区有 户家庭，根据调查数据估计，该小区月均用水量超过 的家庭大约有多少户 ？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是等腰直角三角形，∠BAC=90°，其中A（-2，0），B（0，1），则直线BC的函数表达式为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，在平面直角坐标系中直线y=x﹣2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．

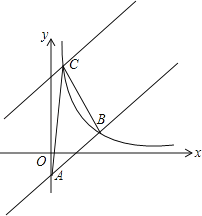
    （1）求反比例函数的关系式；

    （2）将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C，且△ABC的面积为18，求平移后的直线的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

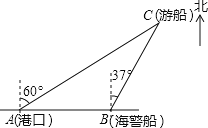
    【题目】一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，

    （1）求点C到直线AB的距离；

    （2）求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．

    （1）证明：AF=CE；

    （2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）

    （2）

    （3）

    （4）

    查看答案和解析>>

    同步练习册答案