
【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
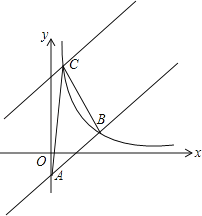
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
【答案】(1)y=![]() ;(2)y=x+7
;(2)y=x+7
【解析】
试题分析:(1)设反比例解析式为y=![]() ,将B坐标代入直线y=x﹣2中求出m的值,确定出B坐标,将B坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
,将B坐标代入直线y=x﹣2中求出m的值,确定出B坐标,将B坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
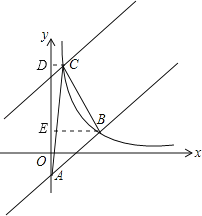
(2)过C作CD垂直于y轴,过B作BE垂直于y轴,设y=x﹣2平移后解析式为y=x+b,C坐标为(a,a+b),三角形ABC面积=梯形BEDC面积+三角形ABE面积﹣三角形ACD面积,由已知三角形ABC面积列出关系式,将C坐标代入反比例解析式中列出关系式,两关系式联立求出b的值,即可确定出平移后直线的解析式.
解:(1)将B坐标代入直线y=x﹣2中得:m﹣2=2,
解得:m=4,
则B(4,2),即BE=4,OE=2,
设反比例解析式为y=![]() ,
,
将B(4,2)代入反比例解析式得:k=8,
则反比例解析式为y=![]() ;
;
(2)设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x﹣2,令x=0求出y=﹣2,得到OA=2,
过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8,
∵S△ABC=S梯形BCDE+S△ABE﹣S△ACD=18,
∴![]() ×(a+4)×(a+b﹣2)+
×(a+4)×(a+b﹣2)+![]() ×(2+2)×4﹣
×(2+2)×4﹣![]() ×a×(a+b+2)=18,
×a×(a+b+2)=18,
解得:a+b=8,
∴a=1,b=7,
则平移后直线解析式为y=x+7.


科目:初中数学 来源: 题型:
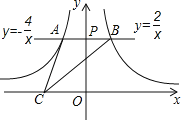
【题目】如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数![]() 的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
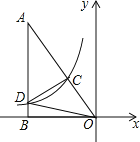
【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=![]() (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年元旦假期,某市各大商场、超市纷纷采取满额减赠、团购等等多种促销方式聚人气,热卖商品主要集中在服装、数码产品、生鲜果蔬等方面.若该市某商场中所有服装均降价20%,且某件服装的原价为x元,则降价后的价格y(元)与原价x(元)之间的函数关系式为( )
A. y=0.8x B. y=0.2x C. y=1.2x D. y=x-0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016海南省第10题)在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
A.(1,2) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①任何有理数的偶次幂都是正数;②倒数等于本身的数有0,-1和1;③用一个平面截正方体最多得到六边形;④所有有理数都能用数轴上的点表示;⑤整式包括单项式和多项式
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐及水面,已知红莲移动的水平距离为2米,这里的水深为( )米.
A.1.5
B.2
C.2.5
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com