练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算

    （1）

    （2）

    （3）

    （4）

    【答案】（1）；（2）；（3）；（4）

    【解析】

    （1）方程去括号，移项合并，将x系数化为1，即可求出解；
    （2）方程去分母，去括号，移项合并，将x系数化为1，即可求出解．

    （3）先把小数化成整数，然后去分母，去括号，移项合并，将x系数化为1，即可求出解．

    （4）方程去分母，去括号，移项合并，将x系数化为1，即可求出解．

    （1）

    去括号得：，

    移项合并得：，

    系数化为1得：；

    （2）

    两边同时乘以6去分母得： ，

    去括号得：，

    移项合并得：，

    系数化为1得：；

    （3）

    整理得：，

    两边同时乘以14去分母得：，

    去括号得：，

    移项合并得：，

    系数化为1得：；

    （4）

    两边同时乘以6去分母得：，

    去括号得：，

    移项合并得：，

    系数化为1得：；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知，两点在数轴上，点表示的数为－10，点到点的距离是点到点距离的3倍，点以每秒3个单位长度的速度从点向右运动.点以每秒2个单位长度的速度从点向右运动（点、同时出发）

    （1）数轴上点对应的数是______.

    （2）经过几秒，点、点分别到原点的距离相等.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点A表示的有理数为，点B表示的有理数为6，点P从点A出发以每秒2个单位长度的速度由运动，同时，点Q从点B出发以每秒1个单位长度的速度由运动，当点Q到达点A时P、Q两点停止运动，设运动时间为单位：秒．

    （1）求时，求点P和点Q表示的有理数；

    （2）求点P与点Q第一次重合时的t值；

    （3）当t的值为多少时，点P表示的有理数与点Q表示的有理数距离是3个单位长度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

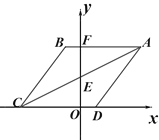
    【题目】如图O为坐标原点，四边形ABCD是菱形，A(4，4)，B点在第二象限，AB＝5，AB与y轴交于点F，对角线AC交y轴于点E

    (1)直接写出B、C点的坐标；

    (2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动，设运动时间为t秒，请用含t的代数式表示△EDP的面积；

    (3)在(2)的条件下，是否存在一点P，使△APE沿其一边翻折构成的四边形是菱形？若存在，请直接写出当t为多少秒时存在符合条件的点P；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

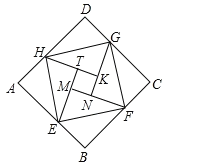
    【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若S1+S2+S3=15，则S2的值是（ ）

    A. 5B. C. D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

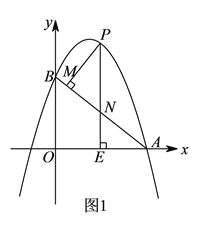
    【题目】如图，抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0)，与y轴交于点B，在X轴上有一动点E(m,0)(0＜m＜8)，过点E作x轴的垂线交直线AB于点N，交抛物线于点P,过点P作PM⊥AB于点M．

    （）分别求出直线AB和抛物线的函数表达式；

    （）设△PMN的面积为S1，△AEN的面积为S2，若S1：S2=36：25，求m的值；

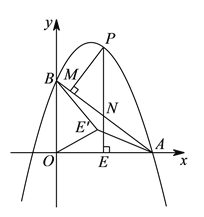
    （）如图2，在（）条件下，将线段OE绕点O逆时针旋转得到OE＇，旋转角为α(0°＜α＜90°)，连接E＇A、E＇B．

    ①在x轴上找一点Q，使△OQE＇∽△OE＇A，并求出Q点的坐标；

    ②求BE＇+AE＇的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】进入夏季用电高峰季节，市供电局维修队接到紧急通知：要到 30 千米远的某乡镇进行紧急抢修，维修工骑摩托车先走，15 分钟后，抢修车装载所需材料出发， 结果两车同时到达抢修点，已知抢修车的速度是摩托车速度的 1.5 倍，求两种车的速 度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

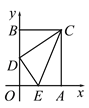
    【题目】如图，在平面直角坐标系中，矩形OACB的顶点O是坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA＝3，OB＝4，D为边OB的中点．若E为边OA上的一个动点，当△CDE的周长最小时，则点E的坐标____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】感知：如图①，在正方形ABCD中，点E在对角线AC上（不与点A、C重合），连结ED，EB，过点E作EF⊥ED，交边BC于点F．易知∠EFC+∠EDC=180°，进而证出EB=EF．
    探究：如图②，点E在射线CA上（不与点A、C重合），连结ED、EB，过点E作EF⊥ED，交CB的延长线于点F．求证：EB=EF
    应用：如图②，若DE=2，CD=1，则四边形EFCD的面积为

    查看答案和解析>>

    同步练习册答案