
【题目】感知:如图①,在正方形ABCD中,点E在对角线AC上(不与点A、C重合),连结ED,EB,过点E作EF⊥ED,交边BC于点F.易知∠EFC+∠EDC=180°,进而证出EB=EF.
探究:如图②,点E在射线CA上(不与点A、C重合),连结ED、EB,过点E作EF⊥ED,交CB的延长线于点F.求证:EB=EF
应用:如图②,若DE=2,CD=1,则四边形EFCD的面积为

【答案】探究:证明见详解;应用:![]()
【解析】
探究:根据正方形的性质得到AB=BC=CD=DA,∠ABC=∠ADC=∠BCD=90°.求得∠ACB=∠ACD=45°,根据全等三角形的性质得到ED=EB,∠EDC=∠EBC,求得∠EFB=∠EDC,根据等腰三角形的判定定理即可得到结论;
应用:连接DF,求得△DEF是等腰直角三角形,根据勾股定理得到CF=![]() ,由三角形的面积公式即可得到结论.
,由三角形的面积公式即可得到结论.
解:探究:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠ADC=∠BCD=90°.
∴∠ACB=∠ACD=45°,
又∵EC=EC,
∴△EDC≌△EBC(SAS),
∴ED=EB,∠EDC=∠EBC,
∵EF⊥ED,
∴∠DEF=90°,
∴∠EFC+∠EDC=180°
又∵∠EBC+∠EBF=180°,
∴∠EFB=∠EDC,
∴∠EBF=∠EFB,
∴EB=EF;
应用:连接DF,

∵EF=DE,∠DEF=90°,
∴△DEF是等腰直角三角形,
∵DE=2,
∴EF=2,DF=![]() ,
,
∵∠DCB=90°,CD=1,
∴CF=![]() ,
,
∴四边形EFCD的面积=S△DEF+S△CDF=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
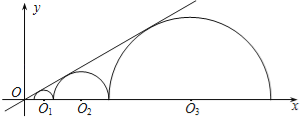
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线![]() 相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
查看答案和解析>>
科目:初中数学 来源: 题型:
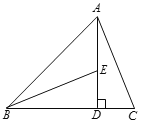
【题目】已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
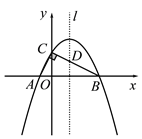
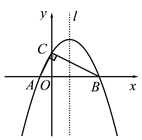
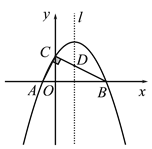
图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从A地出发步行到B地,乙同时从B地步行出发至A地,2小时后在中途相遇,相遇后,甲、乙步行速度都提高了1千米/小时.若设甲刚出发时的速度为a千米/小时,乙刚出发的速度为b千米/小时.
(1)A、B两地的距离可以表示为 千米(用含a,b的代数式表示);
(2)甲从A到B所用的时间是: 小时(用含a,b的代数式表示);
乙从B到A所用的时间是: 小时(用含a,b的代数式表示).
(3)若当甲到达B地后立刻按原路向A返行,当乙到达A地后也立刻按原路向B地返行.甲乙二人在第一次相遇后3小时36分钟又再次相遇,请问AB两地的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.
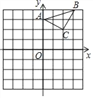
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com