
����Ŀ����ͼ����Rt��ABC�Ķ���A��B��x���ϣ���C��y�����������ϣ���
A(��1��0)��B(4��0)����ACB��90��.
(1)���A��B��C����������߽���ʽ��
(2)�������ߵĶԳ���l��BC�߽��ڵ�D����P�ǶԳ���l�ϵĵ㣬��������P��C��DΪ��������������AOC���ƣ���P������ꣻ
(3)�ڶԳ���l�����������Ƿ�ֱ���ڵ�M��N��ʹ����A��O��M��NΪ������ı�����ƽ���ı��Σ���������ֱ��д����M����N�����ꣻ�������ڣ���˵������.
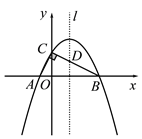
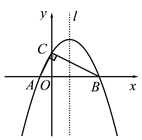
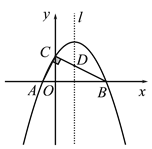
ͼ1 ����ͼ
���𰸡�������
��������������(1)����![]() �����
�����![]() �����꣬�ô���ϵ����������������ߵĽ���ʽ.
�����꣬�ô���ϵ����������������ߵĽ���ʽ.
(2)����������������ۼ���.
(3)����. ����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.�ֵ�ƽ���ı���![]() ��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��⣺(1)��֤![]() ����
����![]() ��
��![]()
��OC=2����C(0��2),
�������߹���A(-1��0)��B(4��0)
��˿��������ߵĽ���ʽΪ![]()
��C��(0��2)�����:![]() ����
����![]()
�������ߵĽ���ʽΪ![]()
(2)��ͼ2��
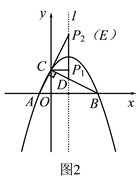
��![]() ʱ��
ʱ��![]() ��P1(
��P1(![]() ��2),
��2),
��![]() ʱ��
ʱ��![]()
��OC��l,
��![]() ��
��
��P2H��![]() ��OC��5��
��OC��5��
��P2 (![]() ��5)
��5)
���P�������Ϊ(![]() ��2)��(
��2)��(![]() ��5).
��5).
(3)����.
����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.
��ͼ3��

��ƽ���ı���![]() ��ƽ���ı���ʱ��M(
��ƽ���ı���ʱ��M(![]() ��
��![]() )��
)��![]() (
(![]() ,
,![]() ),
),
��ƽ���ı���AONM��ƽ���ı���ʱ��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ),
),
��ͼ4�����ı���AMONΪƽ���ı���ʱ��MN��OA����ƽ�֣���ʱ����M(![]() ��m)����
��m)���� ![]()

����N��������![]() �ϣ�
�ϣ�
��-m��-![]() ��(-
��(-![]() +1)( -
+1)( -![]() -4)=-
-4)=-![]() ,
,
��m=![]() ,
,
��ʱM(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).
����������M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() )��M(
)��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ) �� M(
) �� M(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ļ��õ�߷弾�ڣ��й����ά�ӽӵ�����֪ͨ��Ҫ�� 30 ǧ��Զ��ij������н������ޣ�ά����Ħ�г����ߣ�15 ���Ӻ�����װ��������ϳ����� �������ͬʱ�������㣬��֪�������ٶ���Ħ�г��ٶȵ� 1.5 ���������ֳ����� �ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016�Ĵ�ʡ�㰲�У�ijˮ�������ƻ�װ�˼ס��ҡ�������ˮ����������ۣ�ÿ�������涨���أ�����ֻװһ��ˮ���������Ϊװ�˼ס��ҡ�������ˮ��������������

��1����8������װ���ҡ�������ˮ����22�ֵ�A�����ۣ���װ���ҡ�������ˮ������������������
��2��ˮ�����ؼƻ���20������װ�˼ס��ҡ�������ˮ����72�ֵ�B�����ۣ�ÿ��ˮ��������һ����������װ�˼�ˮ��������Ϊm������װ���ҡ�������ˮ�������������������������m��ʾ��
��3���ڣ�2���ʵĻ����ϣ���ΰ���װ�˿�ʹˮ�����ػ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�٣���������ABCD�У���E�ڶԽ���AC�ϣ������A��C�غϣ�������ED��EB������E��EF��ED������BC�ڵ�F����֪��EFC+��EDC=180�㣬����֤��EB=EF��
̽������ͼ�ڣ���E������CA�ϣ������A��C�غϣ�������ED��EB������E��EF��ED����CB���ӳ����ڵ�F����֤��EB=EF
Ӧ�ã���ͼ�ڣ���DE=2��CD=1�����ı���EFCD�����Ϊ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90�㣬AC��BC����BAC��ƽ����AD��BC�ڵ�D���ֱ����A��AE��BC������B��BE��AD��AE��BE�ཻ�ڵ�E����CD��2�����ı���ADBE�������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������A��B��C�����㣬���DZ�ʾ�����ֱ��ǣ�24����10��10.A��B�����ľ����Ϊ��AB����
![]()
(1)��գ�AB= ��BC= ��
(2)����A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��3����λ ���Ⱥ�7����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt���ú�t�Ĵ���ʽ��ʾBC��AB�ij�����̽����BC - AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿��˵�����ɣ�
(3)���ж���P��Q����A���������P��ÿ��1����λ���ȵ��ٶ����յ�C�ƶ�������P �ƶ���B��ʱ����Q�Ŵ�A�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����C��ʱ����Q��ֹͣ�ƶ������P�ƶ���ʱ��Ϊt�룬�ʣ���tΪ����ʱP��Q�������6����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��̽�����֣���ͼ1����֪Rt��ABC�У���ACB��90�㣬AC��BC��ֱ��l����C������A��AD��l������B��BE��l������ֱ�ΪD��E����֤��AD��CE��CD��BE��
��2��Ǩ��Ӧ�ã���ͼ2����һ�����ֱ�ǵ����ǰ�MON����ƽ��ֱ������ϵ�ڣ����ǰ��һ����ǵĶ���������ԭ��O�غϣ���������������ڵ�һ�����ڣ���֪��M������Ϊ��1��3�������N�����꣮
��3����չӦ�ã���ͼ3����ƽ��ֱ������ϵ�ڣ���ֱ֪��y����3x+3��y�ύ�ڵ�P����x�ύ�ڵ�Q����ֱ��PQ��P������ʱ�뷽����ת45������õ�ֱ�߽�x���ڵ�R�����R�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��B=30�㣬��AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ����ǣ�������
��AD�ǡ�BAC��ƽ���ߣ��ڡ�ADC=60�㣻�۵�D��AB�Ĵ�ֱƽ�����ϣ�

A.0B.1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������a��b�������ϵ�λ����ͼ��ʾ��
��1���������ϱ����a����b��λ�ã����Ƚ�a��b����a����b�Ĵ�С��
��2������|a+b|+|a��b|��
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com