
【题目】(1)探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.
(2)迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.

【答案】(1)见解析(2)(4,2)(3)(6,0)
【解析】
(1)先判断出∠ACB=∠ADC,再判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;
(2)先判断出MF=NG,OF=MG,进而得出MF=1,OF=3,即可求出FG=MF+MG=1+3=4,即可得出结论;
(3)先求出OP=3,由y=0得x=1,进而得出Q(1,0),OQ=1,再判断出PQ=SQ,即可判断出OH=4,SH=0Q=1,进而求出直线PR的解析式,即可得出结论.
证明:∵∠ACB=90°,AD⊥l
∴∠ACB=∠ADC
∵∠ACE=∠ADC+∠CAD,∠ACE=∠ACB+∠BCE
∴∠CAD=∠BCE,
∵∠ADC=∠CEB=90°,AC=BC
∴△ACD≌△CBE,
∴AD=CE,CD=BE,

(2)解:如图2,过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,交FM的延长线于G,
由已知得OM=ON,且∠OMN=90°
∴由(1)得MF=NG,OF=MG,
∵M(1,3)
∴MF=1,OF=3
∴MG=3,NG=1
∴FG=MF+MG=1+3=4,
∴OF﹣NG=3﹣1=2,
∴点N的坐标为(4,2),

(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,
对于直线y=﹣3x+3,由x=0得y=3
∴P(0,3),
∴OP=3
由y=0得x=1,
∴Q(1,0),OQ=1,
∵∠QPR=45°
∴∠PSQ=45°=∠QPS
∴PQ=SQ
∴由(1)得SH=OQ,QH=OP
∴OH=OQ+QH=OQ+OP=3+1=4,SH=OQ=1
∴S(4,1),
设直线PR为y=kx+b,则![]() ,解得
,解得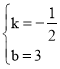
∴直线PR为y=﹣![]() x+3
x+3
由y=0得,x=6
∴R(6,0).


科目:初中数学 来源: 题型:
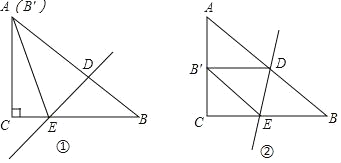
【题目】在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是斜边AB和直角边BC上的点,把△ABC沿着直线DE折叠,顶点B的对应点是点B′.
(1)如图①,如果点B′和点A重合,求CE的长.
(2)如图②,如果点B′落在直角边AC的中点上,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
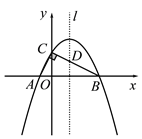
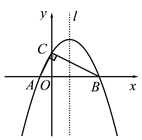
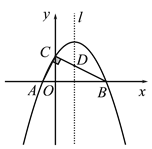
图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答其后的问题:
我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=![]() .
.
(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b=5,c=7,则△ABC的面积为 ;
(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求该块草地的面积.
m,∠A=60°,求该块草地的面积.
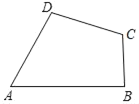
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从A地出发步行到B地,乙同时从B地步行出发至A地,2小时后在中途相遇,相遇后,甲、乙步行速度都提高了1千米/小时.若设甲刚出发时的速度为a千米/小时,乙刚出发的速度为b千米/小时.
(1)A、B两地的距离可以表示为 千米(用含a,b的代数式表示);
(2)甲从A到B所用的时间是: 小时(用含a,b的代数式表示);
乙从B到A所用的时间是: 小时(用含a,b的代数式表示).
(3)若当甲到达B地后立刻按原路向A返行,当乙到达A地后也立刻按原路向B地返行.甲乙二人在第一次相遇后3小时36分钟又再次相遇,请问AB两地的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
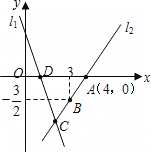
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
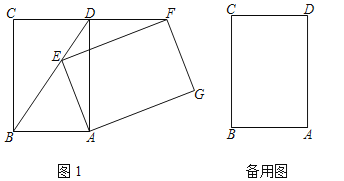
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( ).
A.平均数为251mL B.中位数为249mL
C.众数为250mL D.方差为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com