
【题目】阅读下列材料,并解答其后的问题:
我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=![]() .
.
(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b=5,c=7,则△ABC的面积为 ;
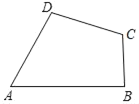
(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求该块草地的面积.
m,∠A=60°,求该块草地的面积.
【答案】(1)![]() (2)(12
(2)(12![]() +24+5
+24+5![]() )m2
)m2
【解析】
(1)由已知△ABC的三边a=4,b=5,c=7,可知这是一个一般的三角形,故选用海伦-奏九韶公式求解即可;(2)过点D作DE⊥AB,垂足为E,连接BD.将所求四边形的面积转化为三个三角形的面积的和进行计算。
(1)解:△ABC的面积为S=![]() =
=![]() =4
=4![]()
故答案是:4![]() ;
;
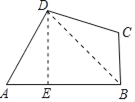
(2)解:如图:过点D作DE⊥AB,垂足为E,连接BD(如图所示)
在Rt△ADE中,
∵∠A=60°,
∴∠ADE=30°,
∴AE=![]() AD=2
AD=2![]()
∴BE=AB﹣AE=2![]() +4
+4![]() ﹣2
﹣2![]() =4
=4![]()
DE=![]()
∴BD=![]()
∴S△BCD=![]()
∵S△ABD=![]()
∴S四边形ABCD=S△BCD+S△ABD= ![]()
答:该块草地的面积为(![]() )m2.
)m2.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
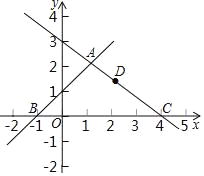
【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=BC,∠BAC的平分线AD交BC于点D,分别过点A作AE∥BC,过点B作BE∥AD,AE与BE相交于点E.若CD=2,则四边形ADBE的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.
(2)迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10 ,B点对应的数为90.

(1)请写出AB的中点M对应的数.
(2)现在有一只电子蚂蚁P从B点出发,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,
①你知道经过几秒两只电子蚂蚁相遇?
②点C对应的数是多少?
③经过多长时间两只电子蚂蚁在数轴上相距10个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
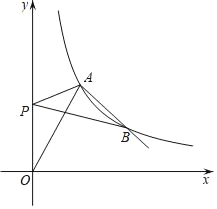
【题目】如图,函数y=![]() 的图象与双曲线y=
的图象与双曲线y=![]() (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com