
【题目】如图,函数y=![]() 的图象与双曲线y=
的图象与双曲线y=![]() (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
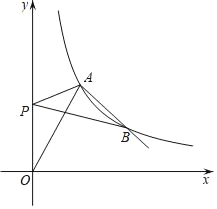
【答案】(1)双曲线的解析式为y=![]() ,点B的坐标为(6,3);点P的坐标为(0,5).
,点B的坐标为(6,3);点P的坐标为(0,5).
【解析】分析:(1)由一次函数的解析式可得点A的坐标,从而求出反比例函数的解析式,解由一次函数与反比例函数的解析式组成的方程组可求点B的坐标;(2)作点A关于y轴的对称点A′,连接A′B,直线A′B与y的交点即为点P,用待定系数法求直线A′B的解析式后即可求点P的坐标.
详解:(1)把A(3,m)代入y=2x,可得m=2×3=6,∴A(3,6),
把A(3,6)代入y=![]() ,可得k=3×6=18,
,可得k=3×6=18,
∴双曲线的解析式为y=![]() ;
;
当x>3时,解方程组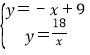 ,可得
,可得![]() 或
或![]() (舍去)
(舍去)
∴点B的坐标为(6,3).
(2)如图所示,作点A关于y轴的对称点A′(-3,6),连接A′P,则A′P=AP,
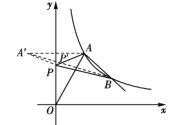
∴PA+PB=A′P+BP≥A′B
当A′,P,B三点共线时,PA+PB的最小值等于A′B的长.
设A′B的解析式为y=ax+b,
把A′(-3,6),B(6,3)代入,可得![]() ,解得
,解得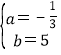 .
.
∴A′B的解析式为y=![]() x+5,
x+5,
令x=0,则y=5,
∴点P的坐标为(0,5).


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答其后的问题:
我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=![]() .
.
(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b=5,c=7,则△ABC的面积为 ;
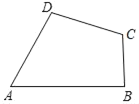
(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求该块草地的面积.
m,∠A=60°,求该块草地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
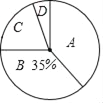
【题目】2017年4月15日至5月15日,某市约8万名初三毕业生参加了中考体育测试,为了了解今年初三毕业生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 27~30 | 24 | 0.4 |
B | 23~26 | m | x |
C | 19~22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合计 | 60 | 1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= ,n= ,x= ,y= ;
(2)在扇形图中,B等级所对应的圆心角是 度;
(3)请你估计某市这8万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( ).
A.平均数为251mL B.中位数为249mL
C.众数为250mL D.方差为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:

有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是_______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.请用其中两个关系式作为条件,另一个作为结论,写出所有正确的结论.
⑵.选择(1)中你写出的一个正确结论,说明它正确的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论错误的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度数不变,始终等于60°
D.当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形
秒时,△PBQ为直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com