练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知四边形ABCD是边长为4的正方形，E为AB的中点，将△ADE绕点D沿逆时针方向旋转后得到△DCF，连接EF，则EF的长为（　　）

    A. 2 B. 2 C. 2 D. 2

    【答案】D

    【解析】

    先利用勾股定理计算出DE，再根据旋转的性质得∠EDF=∠ADC=90°，DE=DF，则可判断△DEF为等腰直角三角形，然后根据等腰直角三角形的性质计算EF的长．

    ∵E为AB的中点，AB=4，∴AE=2，

    ∴DE==2．

    ∵四边形ABCD为正方形，∴∠A=∠ADC=90°，∴∠ADE+∠EDC=90°．

    ∵△ADE绕点D沿逆时针方向旋转后得到△DCF，∴∠ADE=∠CDF，DE=DF，∴∠CDF+∠EDC=90°，∴△DEF为等腰直角三角形，∴EF=DE=2．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

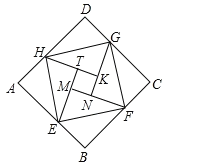
    【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若S1+S2+S3=15，则S2的值是（ ）

    A. 5B. C. D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．

    （1）求甲、乙两种商品每件的进价分别是多少元？

    （2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2016四川省广安市）某水果积极计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．如表为装运甲、乙、丙三种水果的重量及利润．

    （1）用8辆汽车装运乙、丙两种水果共22吨到A地销售，问装运乙、丙两种水果的汽车各多少辆？

    （2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）

    （3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

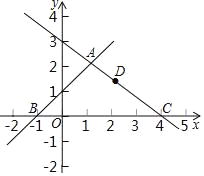
    【题目】如图，在平面直角坐标系可中，直线y＝x+1与y＝﹣x+3交于点A，分别交x轴于点B和点C，点D是直线AC上的一个动点．

    (1)求点A，B，C的坐标；

    (2)在直线AB上是否存在点E使得四边形EODA为平行四边形？存在的话直接写出的值，不存在请说明理由；

    (3)当△CBD为等腰三角形时直接写出D坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】感知：如图①，在正方形ABCD中，点E在对角线AC上（不与点A、C重合），连结ED，EB，过点E作EF⊥ED，交边BC于点F．易知∠EFC+∠EDC=180°，进而证出EB=EF．
    探究：如图②，点E在射线CA上（不与点A、C重合），连结ED、EB，过点E作EF⊥ED，交CB的延长线于点F．求证：EB=EF
    应用：如图②，若DE=2，CD=1，则四边形EFCD的面积为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C＝90°，AC＝BC，∠BAC的平分线AD交BC于点D，分别过点A作AE∥BC，过点B作BE∥AD，AE与BE相交于点E．若CD＝2，则四边形ADBE的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）探索发现：如图1，已知Rt△ABC中，∠ACB＝90°，AC＝BC，直线l过点C，过点A作AD⊥l，过点B作BE⊥l，垂足分别为D、E．求证：AD＝CE，CD＝BE．

    （2）迁移应用：如图2，将一块等腰直角的三角板MON放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O重合，另两个顶点均落在第一象限内，已知点M的坐标为（1，3），求点N的坐标．

    （3）拓展应用：如图3，在平面直角坐标系内，已知直线y＝﹣3x+3与y轴交于点P，与x轴交于点Q，将直线PQ绕P点沿逆时针方向旋转45°后，所得的直线交x轴于点R．求点R的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是正方形ABCD的对角线BD上的一点，连接PA，PC.

    （1）证明：∠PAB=∠PCB;

    （2）在BC上截取一点E，连接PE，使得PE=PC，连接AE，判断△PAE的形状，并说明理由.

    查看答案和解析>>

    同步练习册答案