
【题目】如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15,则S2的值是( )
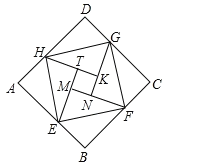
A. 5B. ![]() C.
C. ![]() D. 3
D. 3
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】任何一个整数N,可以用一个多项式来表示:
![]() ,例如:325=3×102+2×10+5.
,例如:325=3×102+2×10+5.
一个正两位数的个位数字是x,十位数字是y.
(1)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被11整除;
(2)若![]() 试求出符合条件的所有两位数.
试求出符合条件的所有两位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:
(1)水蜜桃进价为每箱多少元?
(2)乙超市获利多少元?哪种销售方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1-S2+S3+S4等于( )
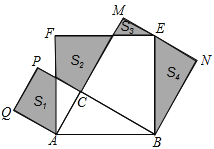
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
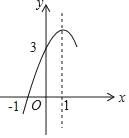
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
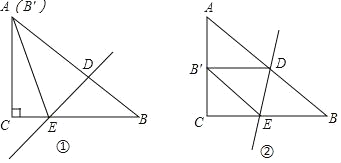
【题目】在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是斜边AB和直角边BC上的点,把△ABC沿着直线DE折叠,顶点B的对应点是点B′.
(1)如图①,如果点B′和点A重合,求CE的长.
(2)如图②,如果点B′落在直角边AC的中点上,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com