
ЁОЬтФПЁПЮоЮ§бєЩНЫЎУлЬвЩЯЪаКѓЃЌМзЁЂввСНГЌЪаЗжБ№гУ60000дЊвдЯрЭЌЕФНјМлЙКНјЯрЭЌЯфЪ§ЕФЫЎУлЬвЃЌМзГЌЪаЯњЪлЗНАИЪЧЃКНЋЫЎУлЬвАДЗжРрАќзАЯњЪлЃЌЦфжаЬєГігХжЪДѓИіЕФЫЎУлЬв400ЯфЃЌвдНјМлЕФ2БЖМлИёЯњЪлЃЌЪЃЯТЕФЫЎУлЬввдИпгкНјМл10%ЯњЪлЃЎввГЌЪаЕФЯњЪлЗНАИЪЧЃКВЛНЋЫЎУлЬвЗжРрЃЌжБНгЯњЪлЃЌМлИёАДМзГЌЪаЗжРрЯњЪлЕФСНжжЫЎУлЬвЪлМлЕФЦНОљЪ§ЖЈМлЃЎШєСНГЌЪаНЋЫЎУлЬвШЋВПЪлЭъЃЌЦфжаМзГЌЪаЛёРћ42000дЊ(ЦфЫќГЩБОВЛМЦ)ЃЎЮЪЃК
(1)ЫЎУлЬвНјМлЮЊУПЯфЖрЩйдЊЃП
(2)ввГЌЪаЛёРћЖрЩйдЊЃПФФжжЯњЪлЗНЪНИќКЯЫуЃП
ЁОД№АИЁП(1)ЫЎУлЬвНјМлЮЊУПЯф100дЊЃЛ (2)ввГЌЪаЛёРћЮЊ33000дЊЃЌМзжжЯњЪлЗНЪНЛёРћЖрЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЫЎУлЬвНјМлЮЊУПЯфxдЊЃЌИљОнРћШѓ=ЃЈЪлМл-НјМлЃЉЁСЯфЪ§ЃЌРћгУМзГЌЪаЛёРћ42000дЊСаЗжЪНЗНГЬМДПЩЧѓГіxЕФжЕЃЌМьбщМДПЩЕУД№АИЃЛЃЈ2ЃЉИљОнНјМлПЩЕУМзГЌЪаЕФЪлМлЃЌМДПЩЧѓГіввГЌЪаЕФЪлМлЃЌИљОнНјМлКЭзмМлПЩЧѓГіЙКНјЯфЪ§ЃЌМДПЩЧѓГіввГЌЪаЕФРћШѓЃЌгы42000дЊБШНЯМДПЩЕУД№АИ.
ЩшЫЎУлЬвНјМлЮЊУПЯфxдЊЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃКx=100ЃЌ
ОМьбщx=100ЪЧЗжЪНЗНГЬЕФНтЃЌЧвЗћКЯЬтвтЃЌ
дђЫЎУлЬвНјМлЮЊУПЯф100дЊЃЛ
(2)ЁпЬєГігХжЪДѓИіЕФЫЎУлЬввдНјМлЕФ2БЖМлИёЯњЪлЃЌЪЃЯТЕФЫЎУлЬввдИпгкНјМл10%ЯњЪлЃЎ
ЁрМзГЌЪаЫЎУлЬвЕФЪлМлЪЧ200дЊ/ЯфКЭ110дЊ/ЯфЃЌ
ЁрввГЌЪаЪлМлЮЊ![]() ЃЌ
ЃЌ
ЁпМзЁЂввСНГЌЪаЗжБ№гУ60000дЊвдЯрЭЌЕФНјМлЙКНјЯрЭЌЯфЪ§ЕФЫЎУлЬвЃЌ
ЁрввГЌЪаЙКНјЫЎУлЬвЃК60000ЁТ100=600ЃЈЯфЃЉ
ЁрввГЌЪаЛёРћЮЊ600ЁС(155-100)=33000(дЊ)ЃЌ
Ёп42000дЊ>33000дЊЃЌ
ЁрМзжжЯњЪлЗНЪНЛёРћЖрЃЎ


 аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ
аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊA=3a2b-2ab2+abcЃЌаЁУїЭЌбЇДэНЋЁА2A-BЁБПДГЩЁА2A+BЁБЃЌЫуЕУНсЙћЮЊ4a2b-3ab2+4abcЃЎ
ЃЈ1ЃЉЧѓГі2A-BЕФНсЙћЃЛ
ЃЈ2ЃЉаЁЧПЭЌбЇЫЕЃЈ1ЃЉжаЕФНсЙћЕФДѓаЁгыcЕФШЁжЕЮоЙиЃЌе§ШЗТ№ЃПШєa=![]() ЃЌb=
ЃЌb=![]() ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвђЮЊsin30Ёу=![]() ЃЌsin210Ёу=
ЃЌsin210Ёу=![]() ЃЌЫљвдsin210Ёу=sinЃЈ180Ёу+30ЁуЃЉ=Љsin30ЁуЃЛвђЮЊsin45Ёу=
ЃЌЫљвдsin210Ёу=sinЃЈ180Ёу+30ЁуЃЉ=Љsin30ЁуЃЛвђЮЊsin45Ёу=![]() ЃЌsin225Ёу=
ЃЌsin225Ёу=![]() ЃЌЫљвдsin225Ёу=sinЃЈ180Ёу+45ЁуЃЉ=Љsin45ЁуЃЌгЩДЫВТЯыЃЌЭЦРэжЊЃКвЛАуЕиЕБІСЮЊШёНЧЪБгаsinЃЈ180Ёу+ІСЃЉ=ЉsinІСЃЌгЩДЫПЩжЊЃКsin240Ёу=ЃЈЁЁЁЁЃЉ
ЃЌЫљвдsin225Ёу=sinЃЈ180Ёу+45ЁуЃЉ=Љsin45ЁуЃЌгЩДЫВТЯыЃЌЭЦРэжЊЃКвЛАуЕиЕБІСЮЊШёНЧЪБгаsinЃЈ180Ёу+ІСЃЉ=ЉsinІСЃЌгЩДЫПЩжЊЃКsin240Ёу=ЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯЕуAБэЪОЕФгаРэЪ§ЮЊ![]() ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ6ЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ
ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ6ЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ![]() дЫЖЏЃЌЭЌЪБЃЌЕуQДгЕуBГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ
дЫЖЏЃЌЭЌЪБЃЌЕуQДгЕуBГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ![]() дЫЖЏЃЌЕБЕуQЕНДяЕуAЪБPЁЂQСНЕуЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЌЕБЕуQЕНДяЕуAЪБPЁЂQСНЕуЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() ЕЅЮЛЃКУы
ЕЅЮЛЃКУы![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЪБЃЌЧѓЕуPКЭЕуQБэЪОЕФгаРэЪ§ЃЛ
ЪБЃЌЧѓЕуPКЭЕуQБэЪОЕФгаРэЪ§ЃЛ
ЃЈ2ЃЉЧѓЕуPгыЕуQЕквЛДЮжиКЯЪБЕФtжЕЃЛ
ЃЈ3ЃЉЕБtЕФжЕЮЊЖрЩйЪБЃЌЕуPБэЪОЕФгаРэЪ§гыЕуQБэЪОЕФгаРэЪ§ОрРыЪЧ3ИіЕЅЮЛГЄЖШЃП
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABC=ЁЯACBЃЌвдACЮЊжБОЖЕФЁбOЗжБ№НЛABЁЂBCгкЕуMЁЂNЃЌЕуPдкABЕФбгГЄЯпЩЯЃЌЧвЁЯCAB=2ЁЯBCPЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпCPЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШєBC=2![]() ЃЌsinЁЯBCP=
ЃЌsinЁЯBCP=![]() ЃЌЧѓЕуBЕНACЕФОрРыЃЎ
ЃЌЧѓЕуBЕНACЕФОрРыЃЎ
ЃЈ3ЃЉдкЕкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓЁїACPЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
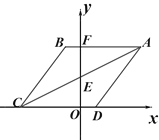
ЁОЬтФПЁПШчЭМOЮЊзјБъдЕуЃЌЫФБпаЮABCDЪЧСтаЮЃЌA(4ЃЌ4)ЃЌBЕудкЕкЖўЯѓЯоЃЌABЃН5ЃЌABгыyжсНЛгкЕуFЃЌЖдНЧЯпACНЛyжсгкЕуE
(1)жБНгаДГіBЁЂCЕуЕФзјБъЃЛ
(2)ЖЏЕуPДгCЕуГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиелЯпЖЮCЉDЉAдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЧыгУКЌtЕФДњЪ§ЪНБэЪОЁїEDPЕФУцЛ§ЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЪЧЗёДцдквЛЕуPЃЌЪЙЁїAPEбиЦфвЛБпЗелЙЙГЩЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыжБНгаДГіЕБtЮЊЖрЩйУыЪБДцдкЗћКЯЬѕМўЕФЕуPЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧгЩЁАедЫЌЯвЭМЁББфЛЏЕУЕНЕФЃЌЫќгЩАЫИіШЋЕШЕФжБНЧШ§НЧаЮЦДНгЖјГЩЃЌМЧЭМжае§ЗНаЮABCDЁЂе§ЗНаЮEFGHЁЂе§ЗНаЮMNKTЕФУцЛ§ЗжБ№ЮЊS1ЁЂS2ЁЂS3ЃЎШєS1+S2+S3=15ЃЌдђS2ЕФжЕЪЧЃЈ ЃЉ
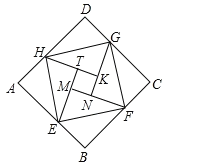
A. 5B. ![]() C.
C. ![]() D. 3
D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНјШыЯФМОгУЕчИпЗхМОНкЃЌЪаЙЉЕчОжЮЌаоЖгНгЕННєМБЭЈжЊЃКвЊЕН 30 ЧЇУздЖЕФФГЯчеђНјааНєМБЧРаоЃЌЮЌаоЙЄЦяФІЭаГЕЯШзпЃЌ15 ЗжжгКѓЃЌЧРаоГЕзАдиЫљашВФСЯГіЗЂЃЌ НсЙћСНГЕЭЌЪБЕНДяЧРаоЕуЃЌвбжЊЧРаоГЕЕФЫйЖШЪЧФІЭаГЕЫйЖШЕФ 1.5 БЖЃЌЧѓСНжжГЕЕФЫй ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2016ЫФДЈЪЁЙуАВЪаЃЉФГЫЎЙћЛ§МЋМЦЛЎзАдЫМзЁЂввЁЂБћШ§жжЫЎЙћЕНЭтЕиЯњЪлЃЈУПСОЦћГЕЙцЖЈТњдиЃЌВЂЧвжЛзАвЛжжЫЎЙћЃЉЃЎШчБэЮЊзАдЫМзЁЂввЁЂБћШ§жжЫЎЙћЕФжиСПМАРћШѓЃЎ

ЃЈ1ЃЉгУ8СОЦћГЕзАдЫввЁЂБћСНжжЫЎЙћЙВ22ЖжЕНAЕиЯњЪлЃЌЮЪзАдЫввЁЂБћСНжжЫЎЙћЕФЦћГЕИїЖрЩйСОЃП
ЃЈ2ЃЉЫЎЙћЛљЕиМЦЛЎгУ20СОЦћГЕзАдЫМзЁЂввЁЂБћШ§жжЫЎЙћЙВ72ЖжЕНBЕиЯњЪлЃЈУПжжЫЎЙћВЛЩйгквЛГЕЃЉЃЌМйЩшзАдЫМзЫЎЙћЕФЦћГЕЮЊmСОЃЌдђзАдЫввЁЂБћСНжжЫЎЙћЕФЦћГЕИїЖрЩйСОЃПЃЈНсЙћгУmБэЪОЃЉ
ЃЈ3ЃЉдкЃЈ2ЃЉЮЪЕФЛљДЁЩЯЃЌШчКЮАВХХзАдЫПЩЪЙЫЎЙћЛљЕиЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com