
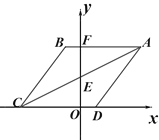
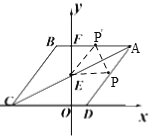
【题目】如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
【答案】(1)B(-1,4),C(-4,0);![]() 见解析;(3)
见解析;(3)![]() 或7.5.
或7.5.
【解析】
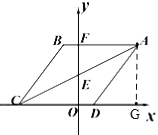
(1)过A作AG⊥x轴于G,根据A点坐标可得AF、AG的长,即可求出BF的长,利用勾股定理可求出DG的长,进而可得OD的长,即可求出OC的长,根据B点在第二象限即可得出B、C两点坐标;(2)根据A、C坐标,利用待定系数法可求出直线AC的解析式,即可求出E点坐标,可得OE=OF,根据菱形的性质可得∠FAE=∠DAE,利用AAS可证明△AEF≌△AEH,可得EH=EF,分别讨论点P在CD、DA边时,利用三角形面积公式表示出△EDP的面积即可;(3)分别讨论沿PA、PE、AE翻折时,点P的位置,画出图形即可得答案.
(1)如图,过A作AG⊥x轴于G,
∵A(4,4),四边形ABCD是菱形,
∴AD=AB=CD=5,AG=OG=4,AG=4,
∴BF=AB-AF=1,DG=![]() =3,
=3,
∴OD=OG-DG=1,
∴OC=CD-OD=4,
∵点B在第二象限,
∴B(-1,4),C(-4,0)
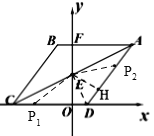
(2)如图,连接DE,过E作EH⊥AD于H,
设AC解析式为y=kx+b,
∵A(4,4),C(-4,0),
∴![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=![]() x+2,
x+2,
当x=0时,y=2,
∴E(0,2),
∴EF=OE=2,
∵四边形ABCD是菱形,
∴∠FAE=∠DAE,
又∵AE=AE,∠AFE=∠AHE=90°,
∴△AEF≌△AEH,
∴EH=EF=2,
∵t=5时,D与P重合,不构成三角形,
∴t≠5,
∴当点P在CD边运动时,即0≤t<5时,S△EDP=![]() DP1×OE=
DP1×OE=![]() (5-t)×2=5-t,
(5-t)×2=5-t,
当点P在DA边运动时,即5<t≤10时,S△EDP=![]() DP2×EH=
DP2×EH=![]() (t-5)×2=t-5.
(t-5)×2=t-5.
(3)当沿AP边翻折时,AE=CE,则P点与C点重合,
∴APE三点在一条直线上,故不符合题意.
如图,当沿PE翻折时,AE=AP,
∵AF=4,EF=2,
∴AE=![]() =
=![]() ,
,
∴AP=![]() ,
,
∴t=10-![]() ,
,
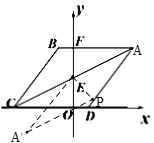
如图,当沿AE翻折时,设PA=AP′=EP′=x,
∵四边形ABCD是菱形,点P在AD上,
∴点P的对称点P′在AB边上,
∴在Rt△EFP′中,x2=22+(4-x)2,
解得:x=2.5,
∴t=10-2.5=7.5.
综上所述:当t为10-![]() 秒或7.5秒时存在符合条件的点P.
秒或7.5秒时存在符合条件的点P.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解 2011 年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:

![]()

(1) 把上面的频数分布表和频数分布直方图补充完整;
(2) 求月均用水量不超过 ![]() 的家庭数占被调查家庭总数的百分比;
的家庭数占被调查家庭总数的百分比;
(3) 若该小区有 ![]() 户家庭,根据调查数据估计,该小区月均用水量超过
户家庭,根据调查数据估计,该小区月均用水量超过 ![]() 的家庭大约有多少户 ?
的家庭大约有多少户 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
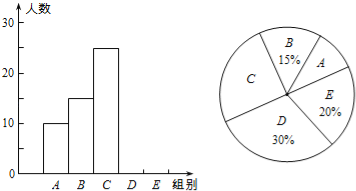
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:
(1)水蜜桃进价为每箱多少元?
(2)乙超市获利多少元?哪种销售方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
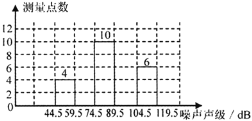
【题目】为了增强环境保护意识,在环保局工作人员指导下,若干名“环保小卫士” 组成了“控制噪声污染”课题学习研究小组.在“世界环境日”当天,该小组抽样 调查了全市 40 个噪声测量点在某时刻的噪声声级(单位:dB),将调查的数据进行
处理(设所测数据均为正整数),得频数分布表如下:
组别 | 噪声声级分组 | 频数 | 频率 |
1 | 44.5~59.5 | 4 | 0.1 |
2 | 59.5~74.5 | a | 0.2 |
3 | 74.5~89.5 | 10 | 0.25 |
4 | 89.5~104.5 | b | c |
5 | 104.5~119.5 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= , b= , c= ;
(2)补充完整频数分布直方图;
(3)如果全市共有 300 个测量点,那么在这一时刻噪声声级小于 75dB 的测量点约有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
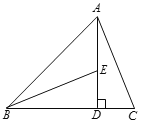
【题目】已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com