
����Ŀ����ͼ���������ϵ�A��ʾ��������Ϊ![]() ����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��2����λ���ȵ��ٶ���
����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��2����λ���ȵ��ٶ���![]() �˶���ͬʱ����Q�ӵ�B������ÿ��1����λ���ȵ��ٶ���
�˶���ͬʱ����Q�ӵ�B������ÿ��1����λ���ȵ��ٶ���![]() �˶�������Q�����AʱP��Q����ֹͣ�˶������˶�ʱ��Ϊ
�˶�������Q�����AʱP��Q����ֹͣ�˶������˶�ʱ��Ϊ![]() ��λ����
�����![]() ��
��
��1����![]() ʱ�����P�͵�Q��ʾ����������
ʱ�����P�͵�Q��ʾ����������
��2�����P���Q��һ���غ�ʱ��tֵ��
��3����t��ֵΪ����ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
![]()
���𰸡�![]() ��P��ʾ����Ϊ
��P��ʾ����Ϊ![]() ����Q��ʾ����Ϊ
����Q��ʾ����Ϊ![]() ��
��![]() ��P���Q��һ���غ�ʱ��tֵΪ4��
��P���Q��һ���غ�ʱ��tֵΪ4��![]() ��t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
��t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�
��������
![]() ����������Եõ���
����������Եõ���![]() ʱ����P�͵�Q��ʾ����������
ʱ����P�͵�Q��ʾ����������
![]() ������������г���������t�ķ��̣��Ӷ��������t��ֵ��
������������г���������t�ķ��̣��Ӷ��������t��ֵ��
![]() ������������г���Ӧ�ķ��̣��Ӷ����Խ���⣮
������������г���Ӧ�ķ��̣��Ӷ����Խ���⣮
![]() ��
��![]() ʱ��
ʱ��
��P��ʾ����Ϊ��![]() ��
��
��Q��ʾ����Ϊ��![]() ��
��
![]()
![]()
![]()
![]() ��
��
�𣺵�P���Q��һ���غ�ʱ��tֵΪ4��
![]() ��P�͵�Q��һ����ǰ��
��P�͵�Q��һ����ǰ��
![]() ��
��
��ã�![]() ��
��
����P�͵�Q������P�����Bǰ��
![]() ��
��
��ã�![]() ��
��
����P�ӵ�B���A�˶�ʱ��
![]() ��
��
��ã�![]() ��
��
���Ͽɵã���t��ֵΪ3��5��9ʱ����P��ʾ�����������Q��ʾ��������������3����λ���ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x=��3�ǹ���x�ķ��̣�k+3��x+2=3x��2k�Ľ⣮
��1����k��ֵ��
��2���ڣ�1���������£���֪�߶�AB=6cm����C��ֱ��AB��һ�㣬��BC=kAC������D��AC���е㣬���߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����AOB�ڲ���һ��P����AOB��60�㣮
��1������P��PC��OB����OA�ڵ�C��
��2������P��PD��OB����OB�ڵ�D����OA�ڵ�E��
��3������C��ֱ��OB�Ĵ��߶�CF��
��4����������ͼ�Σ���ACF���� ���ȣ���OED���� ���ȣ�
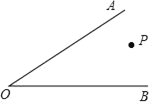
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������߾���A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��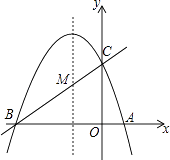
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�����ߵĶԳ���x=��1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ƽ��ֱ������ϵ![]() �У�������������
��������������![]() ��
��![]() �����dz����������������¶��壺
�����dz����������������¶��壺
��![]() �����
�����![]() ���
���![]() �����dz�������Ϊ
�����dz�������Ϊ![]() ��
��
��![]() �����
�����![]() ���
���![]() �����dz�������Ϊ
�����dz�������Ϊ![]() ��
��
���磺��![]() ����
����![]() ����Ϊ
����Ϊ![]() �����Ե�
�����Ե�![]() ���
���![]() �����dz�������Ϊ
�����dz�������Ϊ![]() ��Ҳ����ͼ1���߶�
��Ҳ����ͼ1���߶�![]() ���߶�
���߶�![]() ���ȵĽϴ�ֵ����
���ȵĽϴ�ֵ����![]() Ϊ��ֱ��
Ϊ��ֱ��![]() ���ֱ��
���ֱ��![]() �봹ֱ��
�봹ֱ��![]() ���ֱ��
���ֱ��![]() �Ľ��㣩��
�Ľ��㣩��
��1����֪��![]() ��
��![]() Ϊ
Ϊ![]() ���ϵ�һ�����㣮
���ϵ�һ�����㣮
������![]() ��0��3�������
��0��3�������![]() ���
���![]() �����dz����������� ��
�����dz����������� ��
������![]() ���
���![]() �����dz�������Ϊ2�����
�����dz�������Ϊ2�����![]() ������Ϊ���� ��
���������� ��
��ֱ��д����![]() ���
���![]() �����dz�����������СֵΪ���� ��
�����dz�����������СֵΪ���� ��
��2����֪��![]() ��0��1������
��0��1������![]() ��ֱ��
��ֱ��![]() �ϵ�һ�����㣬��ͼ2�����
�ϵ�һ�����㣬��ͼ2�����![]() ���
���![]() ���dz�����������Сֵ����Ӧ�ĵ�
���dz�����������Сֵ����Ӧ�ĵ�![]() �����꣮
�����꣮
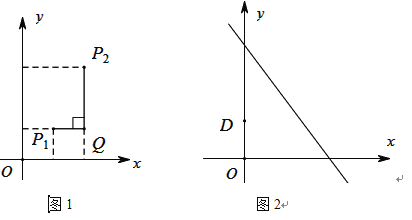
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����E��BC�ߵ��е㣬DE��AC�ཻ�ڵ�F������BF�����н��ۣ���S��ABF=S��ADF����S��CDF=4S��CEF����S��ADF=2S��CEF����S��ADF=2S��CDF �� ������ȷ���ǣ� �� 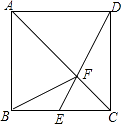
A.�٢�
B.�ڢ�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2�ֱ���10��6������������ÿ��С�����εı߳���Ϊ1��ÿ�������л���һ��ƽ���ı��Σ���ֱ���ͼ1��ͼ2�и���һ���߶Σ���ͼ����������Ҫ��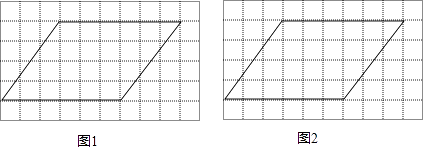
�߶ε�һ���˵�Ϊƽ���ı��εĶ��㣬��һ���˵���ƽ���ı���һ�ߵĸ���ϣ�ÿ��С�����εĶ����Ϊ��㣩��
��ƽ���ı��ηָ������ͼ�Σ�ͼ1��ͼ2�еķַ�������ͬ������Ҫ������һ������Գ�ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͼ����գ���ͼ��

��![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() .��˵����
.��˵����![]() ��
��![]() .�����̲�������.
.�����̲�������.
�⣺��![]() ����֪��
����֪��
��![]() �� ��
�� ��
��![]() ������������
������������
�� �� �� ��
��![]() �� ��
�� ��
����![]() ����֪��
����֪��
�� = ���������� ��
��![]() ��
��![]() �� ��
�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��һ·�����ʺ����߷���̳��5��14���ڱ�����Ļ��ѧУ�ڳ����꼶�����ȡ��50��ͬѧ���С�һ��һ·��֪ʶ���𣬲������ǵľ���ɼ����Ƴ���ͼ������ͳ��ͼ������֪ʶ����ɼ�����λ�����֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com