
【题目】(2016四川省广安市)某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
【答案】(1)装运乙种水果的车有2辆、丙种水果的汽车有6辆;(2)装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆;(3)当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.
【解析】试题分析:(1)根据“8辆汽车装运乙、丙两种水果共22吨到A地销售”列出方程组,即可解答;
(2)设装运乙、丙水果的车分别为a辆,b辆,列出方程组,即可解答;
(3)设总利润为w千元,表示出w=10m+216.列出不等式组,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
试题解析:(1)设装运乙、丙水果的车分别为x辆,y辆,得:![]() ,解得:
,解得:![]() .
.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆.
(2)设装运乙、丙水果的车分别为a辆,b辆,得:![]() ,解得:
,解得:![]() .
.
答:装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆.
(3)设总利润为w千元,w=4×5m+2×7(m﹣12)=4×3(32﹣2m)=10m+216.
∵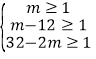 ,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:
(1)水蜜桃进价为每箱多少元?
(2)乙超市获利多少元?哪种销售方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
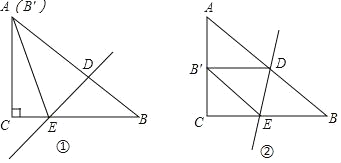
【题目】在Rt△ABC中,∠C=90°,AC=6,BC=8,点D、E分别是斜边AB和直角边BC上的点,把△ABC沿着直线DE折叠,顶点B的对应点是点B′.
(1)如图①,如果点B′和点A重合,求CE的长.
(2)如图②,如果点B′落在直角边AC的中点上,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
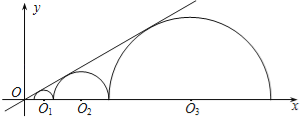
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线![]() 相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a2+b2=10,a+b=4,求a﹣b的值;
(2)关于x的代数式(ax﹣3)(2x+1)﹣4x2+m化简后不含有x2项和常数项,且an+mn=1,求2n3﹣9n2+8n+2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
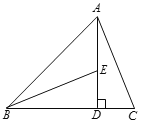
【题目】已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为4的正方形,E为AB的中点,将△ADE绕点D沿逆时针方向旋转后得到△DCF,连接EF,则EF的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的顶点A、B在x轴上,点C在y轴上正半轴上,且
A(-1,0),B(4,0),∠ACB=90°.
(1)求过A、B、C三点的抛物线解析式;
(2)设抛物线的对称轴l与BC边交于点D,若P是对称轴l上的点,且满足以P、C、D为顶点的三角形与△AOC相似,求P点的坐标;
(3)在对称轴l和抛物线上是否分别存在点M、N,使得以A、O、M、N为顶点的四边形是平行四边形,若存在请直接写出点M、点N的坐标;若不存在,请说明理由.
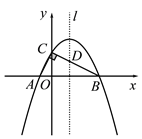
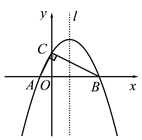
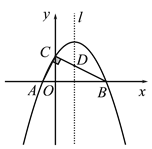
图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
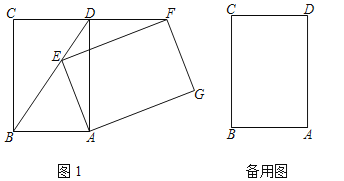
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com