
【题目】在前面的学习中,我们通过对同一面积的不同表达和比较,根据图①和图②发现并验证了平方差公式和完全平方公式.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.
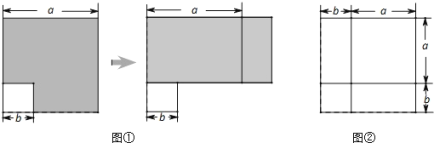
请你利用上述方法解决下列问题:
(1)请写出图1和图2所表示的代数恒等式
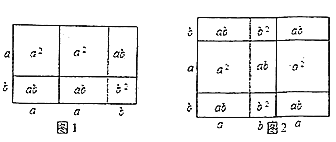
_______ _______
(2)现有a×a,b×b的正方形纸片和a×b的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次,每两个纸片之间既不重叠,也无空隙,拼出的图形中必须保留拼图的痕迹),使拼出的矩形面积为为2a2+5ab+2b2,并标出此矩形的长和宽.
(拓展应用)
提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:用矩形的面积表示两个正数的乘积,以47×43为例:
(1)画长为47,宽为43的矩形,如图③,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面.
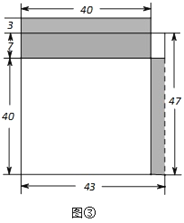
(2)原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,47×43=(40+10)×40+3×7=5×4×100+3×7=2021,
用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述)_________.
证明上述速算方法的正确性;
【答案】(1)(a+b)(2a+b)=2a2+3ab+b2;(2a+b)(a+2b)=2a2+5ab+2b2;(2)图形见解析,矩形的长为:a+2b;宽为:2a+b;归纳提炼:十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,构成运算结果;验证见解析
【解析】
(1)利用面积法即可找到代数恒等式;
(2)根据矩形面积为2a2+5ab+2b2,作出相应的矩形即可求出长和宽;
归纳提炼:根据题意即可写出两个十位数字相同,并且个位数字之和是10的两位数相乘的速算文字表述;设两个十位数字相同,并且个位数字之和是10的两位数的十位数为a,个位数分别是b和(10-b),根据题意与整式的运算法则即可验证.
(1)图1表示的代数恒等式:(a+b)(2a+b)=2a2+3ab+b2;
图2表示的代数恒等式:(2a+b)(a+2b)=2a2+5ab+2b2;
故答案为:(a+b)(2a+b)=2a2+3ab+b2;(2a+b)(a+2b)=2a2+5ab+2b2;
(2)如图,2a2+5ab+2b2=(a+2b) (2a+b)
故矩形的长为:a+2b;宽为:2a+b;
归纳提炼:两个十位数字相同,并且个位数字之和是10的两位数相乘的速算文字表述为:十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,构成运算结果;
验证:设两个十位数字相同,并且个位数字之和是10的两位数的十位数为a,个位数分别是b和(10-b)
则这两个数为分别为:10a+b、10a+10-b,
∴这两个数的乘积为:(10a+b)(10a+10-b)=100a2+100a-10ab+10ab+10b-b2=100a2+100a+10b-b2=100×(a+1)×a+b(10-b);
即十位数字加1的和与十位数字相乘,再乘以100,加上两个个位数字的积,
故验证正确.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】夏天容易发生腹泻等肠道疾病。益阳市医药公司的甲、乙两仓库内分别存有医治腹泻的药品80箱和70箱.现需要将库存的药品凋往南县100箱和沅江50箱,已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示:

(1)设从甲仓库运送到南县的药品为x箱,求总费用y(元)与x(箱)之间的函数关系式.并写出x的取值范围;
(2)求出最低费用,并说明总费用最低时的调配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
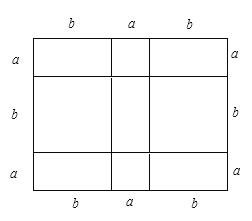
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
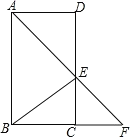
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
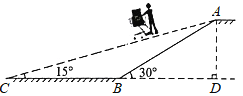
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,并比小明早到达,已知爸爸的平均速度是小明从家到中心书城平均速度的两倍.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(2)小明从中心书城到滨海公园的平均速度是 km/h,
(3)小明爸爸比小明早到达多长时间?
(4)爸爸驾车经过多长时间追上小明?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点0的直线AB交反比例函数y=![]() 的图象于点A,B,点c在反比例函数y=
的图象于点A,B,点c在反比例函数y= ![]() (x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB=
(x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB= ![]() 时,k1,k2应满足的数量关系是( )
时,k1,k2应满足的数量关系是( )
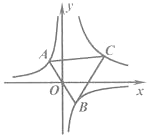
A. k2=2kl B. k2=-2k1 C. k2=4k1 D. k2=-4k1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.

据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生,m的值是 .
(2)请根据据以上信息直在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O 中,点C是![]() 上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
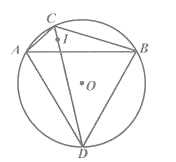
(1)求证:AD=BD.
(2)猜想线段AB与DI的数量关系,并说明理由.
(3)若⊙O的半径为2,点E,F是![]() 的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平整的地面上,用![]() 个棱长都为
个棱长都为![]() 的小正方体堆成一个几何体.
的小正方体堆成一个几何体.
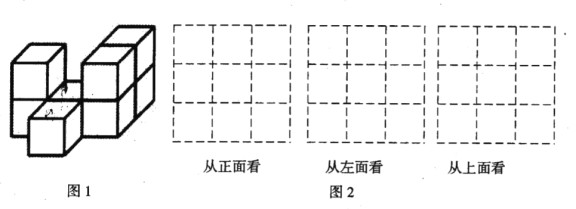
![]() 请在图2中画出从正面、左面和上面看到的这个几何体的形状图;
请在图2中画出从正面、左面和上面看到的这个几何体的形状图;
![]() 如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加 个小正方体;
如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加 个小正方体;
![]() 图1中
图1中![]() 个小正方体搭成的几何体的表面积(包括与地面接触的部分)是
个小正方体搭成的几何体的表面积(包括与地面接触的部分)是 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com