
【题目】在⊙O 中,点C是![]() 上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
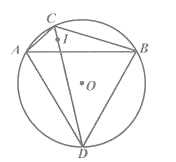
(1)求证:AD=BD.
(2)猜想线段AB与DI的数量关系,并说明理由.
(3)若⊙O的半径为2,点E,F是![]() 的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
【答案】(1)证明见解析;(2)AB=DI,理由见解析(3)![]()
【解析】(1)根据内心的定义可得CI平分∠ACB,可得出角相等,再根据圆周角定理,可证得结论;
(2)根据∠ACB=120°,∠ACD=∠BCD,可求出∠BAD的度数,再根据AD=BD,可证得△ABD是等边三角形,再根据内心的定义及三角形的外角性质,证明∠BID=∠IBD,得出ID=BD,再根据AB=BD,即可证得结论;
(3)连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧,根据已知及圆周角定理、解直角三角形,可求出AD的长,再根据点E,F是 弧AB 的三等分点,△ABD是等边三角形,可证得∠DAI1=∠AI1D,然后利用弧长的公式可求出点I随之运动形成的路径长.
(1)证明:∵点I是∠ABC的内心
∴CI平分∠ACB
∴∠ACD=∠BCD
∴弧AD=弧BD
∴AD=BD
(2)AB=DI
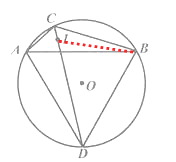
理由:∵∠ACB=120°,∠ACD=∠BCD
∴∠BCD=![]() ×120°=60°
×120°=60°
∵弧BD=弧BD
∴∠DAB=∠BCD=60°
∵AD=BD
∴△ABD是等边三角形,
∴AB=BD,∠ABD=∠C
∵I是△ABC的内心
∴BI平分∠ABC
∴∠CBI=∠ABI
∵∠BID=∠C+∠CBI,∠IBD=∠ABI+∠ABD
∴∠BID=∠IBD
∴ID=BD
∵AB=BD
∴AB=DI
(3)解:如图,连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧

∵∠ACB=120°,弧AD=弧BD
∴∠AED=![]() ∠ACB=
∠ACB=![]() ×120°=60°
×120°=60°
∵圆的半径为2,DE是直径
∴DE=4,∠EAD=90°
∴AD=sin∠AED×DE=![]() ×4=2
×4=2![]()
∵点E,F是 弧AB 的三等分点,△ABD是等边三角形,
∴∠ADB=60°
∴弧AB的度数为120°,
∴弧AM、弧BF的度数都为为40°
∴∠ADM=20°=∠FAB
∴∠DAI1=∠FAB+∠DAB=80°
∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°
∴∠DAI1=∠AI1D
∴AD=I1D=2![]()
∴弧I1I2的长为:![]()


科目:初中数学 来源: 题型:
【题目】在前面的学习中,我们通过对同一面积的不同表达和比较,根据图①和图②发现并验证了平方差公式和完全平方公式.这种利用面积关系解决问题的方法,使抽象的数量关系因几何直观而形象化.
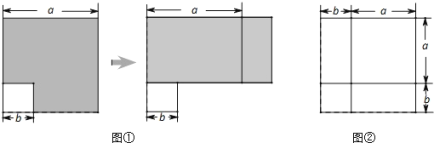
请你利用上述方法解决下列问题:
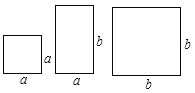
(1)请写出图1和图2所表示的代数恒等式
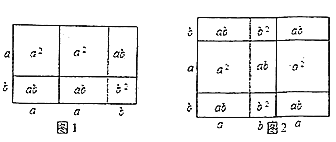
_______ _______
(2)现有a×a,b×b的正方形纸片和a×b的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次,每两个纸片之间既不重叠,也无空隙,拼出的图形中必须保留拼图的痕迹),使拼出的矩形面积为为2a2+5ab+2b2,并标出此矩形的长和宽.
(拓展应用)
提出问题:47×43,56×54,79×71,…是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:用矩形的面积表示两个正数的乘积,以47×43为例:
(1)画长为47,宽为43的矩形,如图③,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形上面.
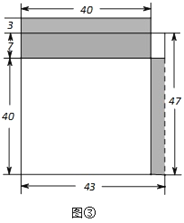
(2)原矩形面积可以有两种不同的表达方式:47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,47×43=(40+10)×40+3×7=5×4×100+3×7=2021,
用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果.
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述)_________.
证明上述速算方法的正确性;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P为四边形ABCD内一点,且满足∠APB+∠CPD=180°, 则称点P为四边形ABCD的一个“互补点”.
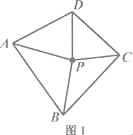
(1)如图1,点P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
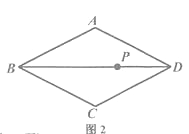
(2)如图2,点P是菱形ABCD对角线上的任意一点.求证:点P为菱形ABCD的一个“互补点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,点
表示的数为-10,点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 距离的3倍,点
距离的3倍,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)数轴上点![]() 对应的数是______.
对应的数是______.
(2)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
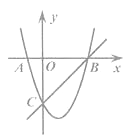
【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.
(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某慈善组织租用甲、乙两种货车共![]() 辆,把蔬菜
辆,把蔬菜![]() 吨,水果
吨,水果![]() 吨,全部运到灾区已知辆甲种货车同时可装蔬菜
吨,全部运到灾区已知辆甲种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨;一辆乙种货车同时可装蔬菜
吨;一辆乙种货车同时可装蔬菜![]() 吨,水果
吨,水果![]() 吨.
吨.
(1)若将这批货物一次性运到灾区,请写出具体的租车方案?
(2)若甲种货车每辆需付燃油费![]() 元,乙种货车每辆需付燃油费
元,乙种货车每辆需付燃油费![]() 元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
元,则应选(1)种的哪种方案,才能使所付的燃油费最少?最少的燃油费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com