
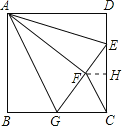
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
【答案】B
【解析】根据翻折变换的性质和正方形的性质可证△ABG≌△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;由于S△FGC=S△GCE-S△FEC,求得面积比较即可.
①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;
②正确.因为:EF=DE=![]() CD=2,设BG=FG=x,则CG=6-x.在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC;
CD=2,设BG=FG=x,则CG=6-x.在直角△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,解得x=3.所以BG=3=6-3=GC;
③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°-∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.过F作FH⊥DC,
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴△EFH∽△EGC,
∴相似比为:![]() ,
,
∴S△FGC=S△GCE-S△FEC=![]() ×3×4-
×3×4-![]() ×4×(
×4×(![]() ×3)=
×3)=![]() .
.
而S△AFE=S△ADE=![]() ,
,
∴S△FGC≠S△AFE
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



查看答案和解析>>
科目:初中数学 来源: 题型:
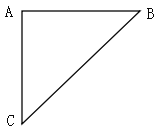
【题目】《九章算术》“勾股”章的问题::“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙各行几何?”大意是说:如图,甲乙二人从A处同时出发,甲的速度与乙的速度之比为7:3,乙一直向东走,甲先向南走十步到达C处,后沿北偏东某方向走了一段距离后与乙在B处相遇,这时,甲乙各走了多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2 ![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( ) 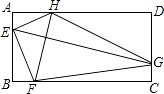
A.8 ![]()
B.8
C.12 ![]()
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是马小哈同学做的一道题:
解方程:![]()
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得![]()
(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC. ①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.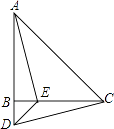
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com