
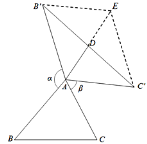
【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



【答案】(1)2;(2)(2)AD=![]() BC,理由见解析;(3)AD′=
BC,理由见解析;(3)AD′=![]() .
.
【解析】(1)首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD=![]() BC.如图,延长AD到E,使得DE=AD,连接B′E,C′E,首先证明四边形AC′EB′是平行四边形,再证明△BAC≌△AB′E,即可解决问题;
BC.如图,延长AD到E,使得DE=AD,连接B′E,C′E,首先证明四边形AC′EB′是平行四边形,再证明△BAC≌△AB′E,即可解决问题;
(3)分情况进行讨论即可得.
(1)∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD=![]() B′C′=
B′C′=![]() BC=
BC=![]() =2,
=2,
故答案为:2;
(2)AD=![]() BC,理由如下:
BC,理由如下:
如图,延长AD至点E,使得DE=AD,
∵B′D=C′D,∴四边形AC′EB′为平行四边形,
∴B′E∥AC′,B′E=AC′=AC,∴∠AB′E+∠B′AC′=180°,
∵α+β=180°,∴∠BAC+∠B′AC′=180°,∴∠AB′E=∠BAC,
∵AB′=AB,∴△AB′E≌△BAC,∴AE=BC,
∴AD=![]() AE=
AE=![]() BC;
BC;
(3)情况一:如图,过点C作△BCE′的中线CF,
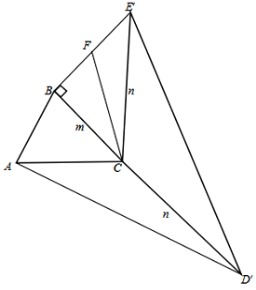
在Rt△BCE′中,由勾股定理
得:![]() ;
;
∴BF=![]() BE′=
BE′=![]() ,
,
在Rt△BCF中,由勾股定理得:CF=![]() =
=![]() =
=![]() ,
,
由(2)可知:AD′=![]() ;
;
情况二:如图,作△CBE′的中线CF并延长到G,使FG=CF,连接BG、E′G,
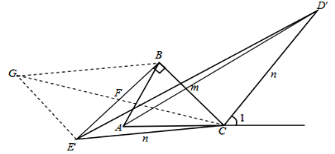
∵BF=E′F,CF=GF,∴四边形BCE′G为平行四边形,
∴BC=GE′,BC∥GE′,∵BC=AC,∴AC=GE′,
由旋转可知∠1=∠BCE′,∵∠1+∠ACD′=180°,∠GE′C+∠BCE′=180°,∴∠ACD′=∠GE′C,
∵CD′=E′C,∴△ACD′≌△GE′C,∴AD′=GC
由情况一可知:BE′=![]() ,AD′=
,AD′=![]() .
.


科目:初中数学 来源: 题型:
【题目】按下面的程序计算,当输入x=100时,输出结果为501;当输入x=20时,输出结果为506;如果开始输入的值x为正数,最后输出的结果为656,那么满足条件的x的值最多有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考:
(1)若点P落在矩形ABCD的边AB上(如图①)
①当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
②当点E在AB上,点F在DC上时(如图②),
求证:四边形DEPF为菱形,并直接写出当AP=3.5时的菱形EPFD的边长.

深入探究
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值 .
拓展延伸
(3)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F. 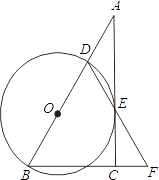
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为 . (精确到1m)
【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】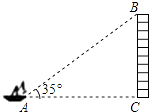
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=![]() ,则CF的长为_______
,则CF的长为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com