
【题目】如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为 . (精确到1m)
【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】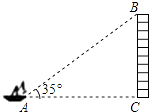
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①最大的负整数是﹣1;②|a|=a;③a+5一定比a大;④38万用科学记数法表示为38×104;⑤单项式﹣![]() 的系数是﹣2,次数是3;⑥﹣
的系数是﹣2,次数是3;⑥﹣![]() <﹣
<﹣![]() ;⑦长方体的截面中,边数最多的多边形是七边形.
;⑦长方体的截面中,边数最多的多边形是七边形.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG. 
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 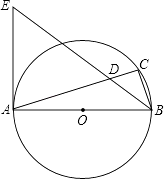
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BO于H.连接OG、CG.
(1)求证:AH=BE;
(2)试探究:∠AGO 的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com