
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

【答案】1
【解析】连接AE,先证明∠BAE的度数为定值,即∠BAE=∠BCP=45°,再根据垂线段最短,当DE⊥AE时,DE最小,此时三角形ADE是等腰直角三角形,解直角三角形可得.
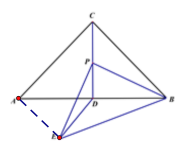
∵△ABC和△EBP均为等腰直角三角形
∴△ABC∽△EBP,且∠ABC=∠EBP=45°
∴![]() ,且∠CBP=∠ABE
,且∠CBP=∠ABE
∴△CBP∽△ABE
∴∠BCP=∠BAE
∵CA=CB,∠ACB=90°,CD⊥AB
∴∠BCP=45°
∴∠BAE=∠BCP=45°
即∠BAE的度数为定值,
当DE⊥AE时,DE最小,此时三角形ADE是等腰直角三角形,
因为,三角形ABC是等腰直角三角形,CA=CB=2,CD⊥AB
所以,AD=![]()
所以,设AE=DE=x,则由AE2+DE2=AD2得,2x2=2,
解得x=1
所以,DE=1.
故答案为:1


科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为![]() ,
,![]() ,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
![]()
![]() 运动前线段AB的长为______;运动1秒后线段AB的长为______;
运动前线段AB的长为______;运动1秒后线段AB的长为______;
![]() 运动t秒后,点A,点B运动的距离分别为______和______;
运动t秒后,点A,点B运动的距离分别为______和______;
![]() 求t为何值时,点A与点B恰好重合;
求t为何值时,点A与点B恰好重合;
![]() 在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.
在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.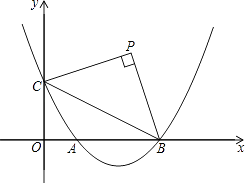
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是马小哈同学做的一道题:
解方程:![]()
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得![]()
(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com