
【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=°. 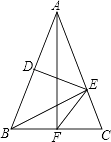
【答案】45
【解析】解:∵DE垂直平分AB, ∴AE=BE,
∵BE⊥AC,
∴△ABE是等腰直角三角形,
∴∠BAE=∠ABE=45°,
又∵AB=AC,
∴∠ABC= ![]() (180°﹣∠BAC)=
(180°﹣∠BAC)= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°,
∵AB=AC,AF⊥BC,
∴BF=CF,
∵EF= ![]() BC(直角三角形斜边中线等于斜边的一半),
BC(直角三角形斜边中线等于斜边的一半),
∴BF=EF=CF,
∴∠BEF=∠CBE=22.5°,
∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.
故答案为:45.
根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,然后求出△ABE是等腰直角三角形,根据等腰直角三角形的性质求出∠BAE=∠ABE=45°,再根据等腰三角形两底角相等求出∠ABC,然后求出∠CBE,根据等腰三角形三线合一的性质可得BF=CF,根据直角三角形斜边上的中线等于斜边的一半可得BF=EF,根据等边对等角求出∠BEF=∠CBE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 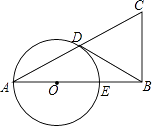
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考:
(1)若点P落在矩形ABCD的边AB上(如图①)
①当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
②当点E在AB上,点F在DC上时(如图②),
求证:四边形DEPF为菱形,并直接写出当AP=3.5时的菱形EPFD的边长.

深入探究
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值 .
拓展延伸
(3)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的课外阅读情况,就“我最喜爱的课外读物”对文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),并根据调查结果绘制了两幅不完整的统计图,请你根据图中提供的信息,解答下列问题: 
(1)这次被调查的学生共有多少名?
(2)请将条形统计图补充完整;并在扇形统计图中,计算出“其他类”所对应的圆心角的度数;
(3)若该校有2400名学生,请你估计该校喜爱“科普类”的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F. 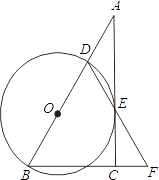
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.仪征市区的公共自行车给市民出行带来不少方便.我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况: A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.
将这次调查情况整理并绘制如下两幅统计图: 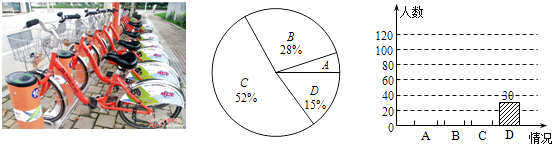
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com