
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 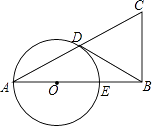
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
【答案】
(1)证明:连接DE,
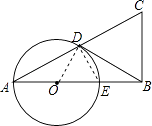
∵AE是直径,
∴∠ADE=90°,
∴∠ADE=∠ABC,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ ![]() ,
,
∴ACAD=ABAE
(2)解:连接OD,

∵BD是⊙O的切线,
∴OD⊥BD,
在RT△OBD中,OE=BE=OD,
∴OB=2OD,
∴∠OBD=30°,
同理∠BAC=30°,
在RT△ABC中,AC=2BC=2×2=4
【解析】(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,将一个由五个边长为1的小正方形组成的图形剪开可以拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)你能在图②中连结四个格点(每一个小正方形的顶点叫做格点),画出一个面积为10的正方形吗?如果不能,请说明理由;如果能,请在图②中画出这个正方形.
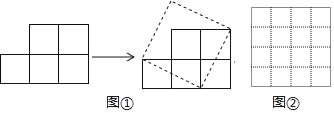
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
查看答案和解析>>
科目:初中数学 来源: 题型:
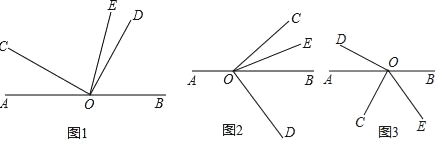
【题目】已知直线AB经过点O,∠COD=90°,OE是∠BOC的平分线.
(1)如图1,若∠AOC=50°,求∠DOE;
(2)如图1,若∠AOC=α,求∠DOE;(用含α的式子表示)
(3)将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其它条件不变,(2)中的结论是否还成立?试说明理由;
(4)将图1中的∠COD绕顶点O逆时针旋转到图3的位置,其它条件不变,求∠DOE.(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ACB=90°,点E为△ABC内一点,且∠BEC=90°,将△BEC绕C点顺时针旋转90°,使BC与AC重合,得到△AFC,连接EF交AC于点M,已知BC=10,CF=6,则AM:MC的值为( ) 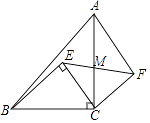
A.4:3
B.3:4
C.5:3
D.3:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.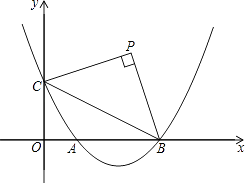
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com