
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.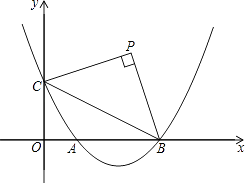
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
【答案】
(1)(b,0);(0, ![]() )
)
(2)
解:存在,
假设存在这样的点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形.
设点P的坐标为(x,y),连接OP.
则S四边形PCOB=S△PCO+S△POB= ![]()
![]() x+
x+ ![]() by=2b,
by=2b,
∴x+4y=16.
过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,
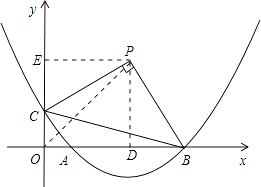
∴∠PEO=∠EOD=∠ODP=90°.
∴四边形PEOD是矩形.
∴∠EPD=90°.
∴∠EPC=∠DPB.
∴△PEC≌△PDB,∴PE=PD,即x=y.
由 ![]() 解得
解得 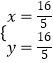
由△PEC≌△PDB得EC=DB,即 ![]() ﹣
﹣ ![]() =b﹣
=b﹣ ![]() ,
,
解得b= ![]() >2符合题意.
>2符合题意.
∴P的坐标为( ![]() ,
, ![]() )
)
(3)
解:假设存在这样的点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似.
∵∠QAB=∠AOQ+∠AQO,
∴∠QAB>∠AOQ,∠QAB>∠AQO.
∴要使△QOA与△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x轴.
∵b>2,
∴AB>OA,
∴∠Q0A>∠ABQ.
∴只能∠AOQ=∠AQB.此时∠OQB=90°,
由QA⊥x轴知QA∥y轴.
∴∠COQ=∠OQA.
∴要使△QOA与△OQC相似,只能∠QCO=90°或∠OQC=90°.
(I)当∠OCQ=90°时,△CQO≌△QOA.
∴AQ=CO= ![]() .
.
由AQ2=OAAB得:( ![]() )2=b﹣1.
)2=b﹣1.
解得:b=8±4 ![]() .
.
∵b>2,
∴b=8+4 ![]() .
.
∴点Q的坐标是(1,2+ ![]() ).
).
(II)当∠OQC=90°时,△OCQ∽△QOA,
∴ ![]() ,即OQ2=OCAQ.
,即OQ2=OCAQ.
又OQ2=OAOB,
∴OCAQ=OAOB.即 ![]() AQ=1×b.
AQ=1×b.
解得:AQ=4,此时b=17>2符合题意,
∴点Q的坐标是(1,4).
∴综上可知,存在点Q(1,2+ ![]() )或Q(1,4),使得△QCO,△QOA和△QAB中的任意两个三角形均相似.
)或Q(1,4),使得△QCO,△QOA和△QAB中的任意两个三角形均相似.

【解析】解:(1)令y=0,即y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() =0,
=0,
解得:x=1或b,
∵b是实数且b>2,点A位于点B的左侧,
∴点B的坐标为(b,0),
令x=0,
解得:y= ![]() ,
,
∴点C的坐标为(0, ![]() ),
),
所以答案是:(b,0),(0, ![]() );
);
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 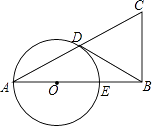
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CA=CB=2,CD⊥AB于D,点P是线段CD上的一个动点,以点P为直角顶点向下作等腰直角△PBE,
连接DE ,则DE的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴l上,一动点Q从原点O出发,沿直线l以每秒钟2个单位长度的速度来回移动,其移动方式是先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…
![]()
(1)求出5秒钟后动点Q所处的位置;
(2)如果在数轴l上还有一个定点A,且A与原点O相距20个单位长度,问:动点Q从原点出发,可能与点A重合吗?若能,则第一次与点A重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=![]() ,则CF的长为_______
,则CF的长为_______

查看答案和解析>>
科目:初中数学 来源: 题型:
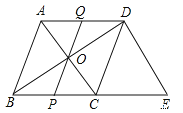
【题目】如图,在菱形ABCD中,对角线AC与BD相交于O点,AB=5,AC=6,过D点作DE//AC交BC的延长线于E点
(1)求△BDE的周长
(2)点P为线段BC上的点,连接PO并延长交AD于点Q,求证:BP=DQ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.仪征市区的公共自行车给市民出行带来不少方便.我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况: A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.
将这次调查情况整理并绘制如下两幅统计图: 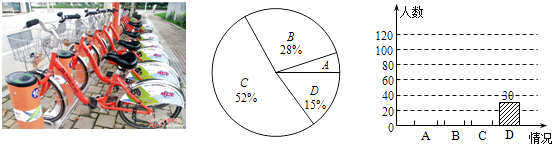
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下面由“※”组成的图案和算式,解答问题:
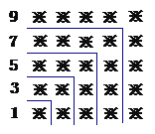
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+ … +19= ;
(2)请猜想:
1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)= ;
(3)请用上述规律计算:
103+105+107+ … +2013+2015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com