
【题目】已知在数轴l上,一动点Q从原点O出发,沿直线l以每秒钟2个单位长度的速度来回移动,其移动方式是先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…
![]()
(1)求出5秒钟后动点Q所处的位置;
(2)如果在数轴l上还有一个定点A,且A与原点O相距20个单位长度,问:动点Q从原点出发,可能与点A重合吗?若能,则第一次与点A重合需多长时间?若不能,请说明理由.
科目:初中数学 来源: 题型:
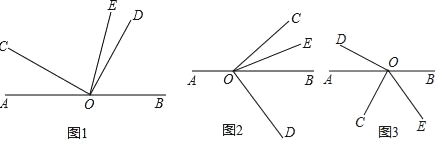
【题目】已知直线AB经过点O,∠COD=90°,OE是∠BOC的平分线.
(1)如图1,若∠AOC=50°,求∠DOE;
(2)如图1,若∠AOC=α,求∠DOE;(用含α的式子表示)
(3)将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其它条件不变,(2)中的结论是否还成立?试说明理由;
(4)将图1中的∠COD绕顶点O逆时针旋转到图3的位置,其它条件不变,求∠DOE.(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为![]() ,
,![]() ,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
![]()
![]() 运动前线段AB的长为______;运动1秒后线段AB的长为______;
运动前线段AB的长为______;运动1秒后线段AB的长为______;
![]() 运动t秒后,点A,点B运动的距离分别为______和______;
运动t秒后,点A,点B运动的距离分别为______和______;
![]() 求t为何值时,点A与点B恰好重合;
求t为何值时,点A与点B恰好重合;
![]() 在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.
在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() (b+1)x+
(b+1)x+ ![]() (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.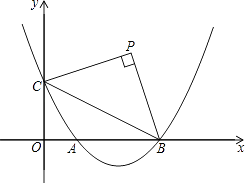
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1. 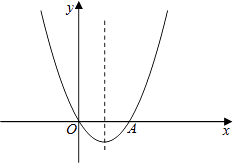
(1)常数m= , 点A的坐标为;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com