
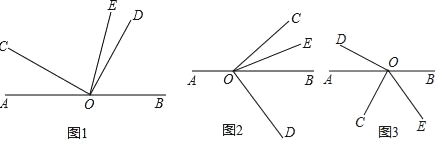
ЁОЬтФПЁПвбжЊжБЯпABОЙ§ЕуOЃЌЁЯCOD=90ЁуЃЌOEЪЧЁЯBOCЕФЦНЗжЯпЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯAOC=50ЁуЃЌЧѓЁЯDOEЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЁЯAOC=ІСЃЌЧѓЁЯDOEЃЛЃЈгУКЌІСЕФЪНзгБэЪОЃЉ
ЃЈ3ЃЉНЋЭМ1жаЕФЁЯCODШЦЖЅЕуOЫГЪБеыа§зЊЕНЭМ2ЕФЮЛжУЃЌЦфЫќЬѕМўВЛБфЃЌЃЈ2ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПЪдЫЕУїРэгЩЃЛ
ЃЈ4ЃЉНЋЭМ1жаЕФЁЯCODШЦЖЅЕуOФцЪБеыа§зЊЕНЭМ3ЕФЮЛжУЃЌЦфЫќЬѕМўВЛБфЃЌЧѓЁЯDOE.ЃЈгУКЌІСЕФЪНзгБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉ25ЁуЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЃЈ2ЃЉжаЕФ
ЃЛЃЈ3ЃЉЃЈ2ЃЉжаЕФ![]() НсТлЛЙГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ4ЃЉ180ЁуЉ
НсТлЛЙГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ4ЃЉ180ЁуЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌИљОнЦННЧЕФЖЈвхКЭЁЯCOD=90ЁуЃЌЕУЁЯAOC+ЁЯBOD=90ЁуЃЌДгЖјЧѓЕУЃКЁЯBOD=40ЁуЃЌгЩНЧЦНЗжЯпЖЈвхЕУЃКЁЯBOE=![]() ЁЯBOC=65ЁуЃЌРћгУНЧЕФВюПЩЕУНсТлЃЛ
ЁЯBOC=65ЁуЃЌРћгУНЧЕФВюПЩЕУНсТлЃЛ
ЃЈ2ЃЉЭЌРэПЩЕУЃКЁЯDOE=![]() ІСЃЛ
ІСЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌИљОнЦННЧЕФЖЈвхЕУЃКЁЯBOC=180Ёу-ІСЃЌгЩНЧЦНЗжЯпЖЈвхЕУЃКЁЯEOC=![]() ЁЯBOC=90Ёу-
ЁЯBOC=90Ёу-![]() ІСЃЌИљОнНЧЕФВюПЩЕУЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂЃЛ
ІСЃЌИљОнНЧЕФВюПЩЕУЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂЃЛ
ЃЈ4ЃЉЭЌРэПЩЕУЃКЁЯDOE=ЁЯCOD+ЁЯCOE=180Ёу-![]() ІСЃЎ
ІСЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁпЁЯCOD=90ЁуЃЌ
ЁрЁЯAOC+ЁЯBOD=90ЁуЃЌ
ЁпЁЯAOC=50ЁуЃЌ
ЁрЁЯBOD=40ЁуЃЌ
ЁрЁЯBOC=ЁЯCOD+ЁЯBOD=90Ёу+40Ёу=130ЁуЃЌ
ЁпOEЦНЗжЁЯBOCЃЌ
ЁрЁЯBOE=![]() ЁЯBOC=65ЁуЃЌ
ЁЯBOC=65ЁуЃЌ
ЁрЁЯDOE=65ЁуЉ40Ёу=25ЁуЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌгЩЃЈ1ЃЉжЊЃКЁЯAOC+ЁЯBOD=90ЁуЃЌ
ЁпЁЯAOC=ІСЃЌ
ЁрЁЯBOD=90ЁуЉІСЃЌ
ЁрЁЯBOC=ЁЯCOD+ЁЯBOD=90Ёу+90ЁуЉІС=180ЁуЉІСЃЌ
ЁпOEЦНЗжЁЯBOCЃЌ
ЁрЁЯBOE=![]() ЁЯBOC =90Љ
ЁЯBOC =90Љ![]() ІСЃЌ
ІСЃЌ
ЁрЁЯDOE=ЁЯBOEЉЁЯBOD=90ЁуЉ![]() ІСЉЃЈ90ЁуЉІСЃЉ=
ІСЉЃЈ90ЁуЉІСЃЉ=![]() ІСЃЌ
ІСЃЌ
ЃЈ3ЃЉЃЌЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂЃЌРэгЩЪЧЃК
ШчЭМ2ЃЌЁпЁЯAOC+ЁЯBOC=180ЁуЃЌЁЯAOC=ІСЃЌ
ЁрЁЯBOC=180ЁуЉІСЃЌ
ЁпOEЦНЗжЁЯBOCЃЌ
ЁрЁЯEOC=![]() ЁЯBOC=90ЁуЉ
ЁЯBOC=90ЁуЉ![]() ІСЃЌ
ІСЃЌ
ЁпЁЯCOD=90ЁуЃЌ
ЁрЁЯDOE=ЁЯCODЉЁЯCOE=90ЁуЉЃЈ90ЁуЉ![]() ІСЃЉ=
ІСЃЉ=![]() ІСЃЛ
ІСЃЛ
ЃЈ4ЃЉШчЭМ3ЃЌЁпЁЯAOC+ЁЯBOC=180ЁуЃЌЁЯAOC=ІСЃЌ
ЁрЁЯBOC=180ЁуЉІСЃЌ
ЁпOEЦНЗжЁЯBOCЃЌ
ЁрЁЯEOC=![]() ЁЯBOC=90ЁуЉ
ЁЯBOC=90ЁуЉ![]() ІСЃЌ
ІСЃЌ
ЁпЁЯCOD=90ЁуЃЌ
ЁрЁЯDOE=ЁЯCOD+ЁЯCOE=90Ёу+ЃЈ90ЁуЉ![]() ІСЃЉ=180ЁуЉ
ІСЃЉ=180ЁуЉ![]() ІСЃЎ
ІСЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЧѓ1+3+32+33+34+35+36+37+38ЕФжЕЪБЃЌеХКьЗЂЯжЃКДгЕкЖўИіМгЪ§Ц№УПвЛИіМгЪ§ЖМЪЧЧАвЛИіМгЪ§ЕФ3БЖЃЌгкЪЧЫ§МйЩшЃКS=1+3+32+33+34+35+36+37+38ЂйЃЌ ШЛКѓдкЂйЪНЕФСНБпЖМГЫвд3ЃЌЕУЃК3S=3+32+33+34+35+36+37+38+39ЂкЃЌ
ЂкЉЂйЕУЃЌ3SЉS=39Љ1ЃЌМД2S=39Љ1ЃЌ
ЫљвдS= ![]() ЃЎ
ЃЎ
ЕУГіД№АИКѓЃЌАЎЖЏФдНюЕФеХКьЯыЃКШчЙћАбЁА3ЁБЛЛГЩзжФИmЃЈmЁй0ЧвmЁй1ЃЉЃЌФмЗёЧѓГі1+m+m2+m3+m4+Ё+m2016ЕФжЕЃПШчФмЧѓГіЃЌЦфе§ШЗД№АИЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮOABCЁЂBDEFЪЧУцЛ§ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЕФе§ЗНаЮЃЌЕуAдкxжсЩЯЃЌЕуFдкBCЩЯЃЌЕуEдкЗДБШР§КЏЪ§
ЕФе§ЗНаЮЃЌЕуAдкxжсЩЯЃЌЕуFдкBCЩЯЃЌЕуEдкЗДБШР§КЏЪ§![]() ЃЈkЃО0ЃЉЕФЭМЯѓЩЯЃЌШє
ЃЈkЃО0ЃЉЕФЭМЯѓЩЯЃЌШє![]() ЃЌдђkжЕЮЊЃЈЁЁЁЁЃЉ
ЃЌдђkжЕЮЊЃЈЁЁЁЁЃЉ

A. 1 B. ![]() C. 2 D. 4
C. 2 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЃКШчЭМЃЈ1ЃЉЃЌЕуEЁЂFЗжБ№дке§ЗНаЮABCDЕФБпBCЁЂCDЩЯЃЌЁЯEAF=45ЁуЃЌЪдХаЖЯBEЁЂEFЁЂFDжЎМфЕФЪ§СПЙиЯЕЃЎ
ЃЈ1ЃЉЁОЗЂЯжжЄУїЁП
аЁДЯАбЁїABEШЦЕуAФцЪБеыа§зЊ90ЁужСЁїADGЃЌДгЖјЗЂЯжEF=BE+FDЃЌЧыФуРћгУЭМЃЈ1ЃЉжЄУїЩЯЪіНсТлЃЎ
ЃЈ2ЃЉЁОРрБШв§ЩъЁП
ШчЭМЃЈ2ЃЉЃЌЫФБпаЮABCDжаЃЌЁЯBADЁй90ЁуЃЌAB=ADЃЌЁЯB+ЁЯD=180ЁуЃЌЕуEЁЂFЗжБ№дкБпBCЁЂCDЩЯЃЌдђЕБЁЯEAFгыЁЯBADТњзуЙиЯЕЪБЃЌШдгаEF=BE+FDЃЎ
ЃЈ3ЃЉЁОЬНОПгІгУЁП
ШчЭМЃЈ3ЃЉЃЌдкФГЙЋдАЕФЭЌвЛЫЎЦНУцЩЯЃЌЫФЬѕЭЈЕРЮЇГЩЫФБпаЮABCDЃЎвбжЊAB=AD=80УзЃЌЁЯB=60ЁуЃЌЁЯADC=120ЁуЃЌЁЯBAD=150ЁуЃЌЕРТЗBCЁЂCDЩЯЗжБ№гаОАЕуEЁЂFЃЌЧвAEЁЭADЃЌDF=40ЃЈ ![]() Љ1ЃЉУзЃЌЯжвЊдкEЁЂFжЎМфаовЛЬѕБЪжБЕРТЗЃЌЧѓетЬѕЕРТЗEFЕФГЄЃЈНсЙћШЁећЪ§ЃЌВЮПМЪ§ОнЃК
Љ1ЃЉУзЃЌЯжвЊдкEЁЂFжЎМфаовЛЬѕБЪжБЕРТЗЃЌЧѓетЬѕЕРТЗEFЕФГЄЃЈНсЙћШЁећЪ§ЃЌВЮПМЪ§ОнЃК ![]() =1.41ЃЌ
=1.41ЃЌ ![]() =1.73ЃЉ
=1.73ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌХзЮяЯпОЙ§ЕуAЃЈ0ЃЌ4ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌCЃЈ5ЃЌ0ЃЉЃЌЦфЖдГЦжсгыxжсЯрНЛгкЕуMЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖдГЦжсЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPABЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉСЌНгACЃЌдкжБЯпACЕФЯТЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдквЛЕуNЃЌЪЙЁїNACЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЕуNЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬт8ЗжЃЉЁїABCдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЌЦфжаУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ИіЕЅЮЛГЄЖШЃЎ
ЃЈ1ЃЉАДвЊЧѓзїЭМЃК
ЂйЛГіЁїABCЙигкдЕуOЕФжааФЖдГЦЭМаЮЁїA1B1C1ЃЛ
ЂкЛГіНЋЁїABCШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНЁїAB2C2ЃЌ
ЃЈ2ЃЉЛиД№ЯТСаЮЪЬтЃК
ЂйЁїA1B1C1жаЖЅЕуA1зјБъЮЊ ЃЛЂкШєPЃЈaЃЌbЃЉЮЊЁїABCБпЩЯвЛЕуЃЌдђАДееЃЈ1ЃЉжаЂйзїЭМЃЌЕуPЖдгІЕФЕуP1ЕФзјБъЮЊ ЃЎ

ЁОД№АИЁПЃЈ1ЃЉзїЭММћНтЮіЃЛЃЈ2ЃЉЃЈ1ЃЌ-2ЃЉЃЈ-a,-bЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШевГіЖдгІЕуЕФЮЛжУЃЌдйЫГДЮСЌНгМДПЩЃЛ
ЃЈ2ЃЉЂйИљОнЭМаЮПЩжБНгаДГізјБъЃЛЂкИљОнЙигкдЕуЖдГЦЕуЕФзјБъЬиЕуПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМЫљЪОЃК
ЃЈ2ЃЉЂйИљОнЭМаЮПЩЕУA1зјБъЮЊЃЈ2ЃЌЉ4ЃЉЃЛ
ЂкЕуP1ЕФзјБъЮЊЃЈЉaЃЌЉbЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈЉ2ЃЌЉ4ЃЉЃЛЃЈЉaЃЌЉbЃЉЃЎ

ПМЕуЃКзїЭМ-а§зЊБфЛЛЃЎ
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
23
ЁОЬтФПЁПдкбЇЯАСЫЁАЦеВщгыГщбљЕїВщЁБжЎКѓЃЌФГаЃАЫЃЈ1ЃЉАрЪ§бЇаЫШЄаЁзщЖдИУаЃбЇЩњЕФЪгСІЧщПіНјааСЫГщбљЕїВщЃЌВЂЛГіСЫШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМЃЎЧыИљОнЭМжааХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщВщЛюЖЏжаЙВГщВщСЫЁЁЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉвбжЊИУаЃЦпФъМЖЁЂАЫФъМЖЁЂОХФъМЖбЇЩњЪ§ЗжБ№ЮЊ360ШЫЁЂ400ШЫЁЂ540ШЫЃЎ
ЂйЪдЙРЫуЃКИУаЃОХФъМЖЪгСІВЛЕЭгк4.8ЕФбЇЩњдМгаЁЁЁЁУћЃЛ
ЂкЧыФуАяУІЙРЫуГіИУаЃЪгСІЕЭгк4.8ЕФбЇЩњЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЁїABCжаЃЌЁЯB=90ЁуЃЌвдABЩЯЕФвЛЕуOЮЊдВаФЃЌвдOAЮЊАыОЖЕФдВНЛACгкЕуDЃЌНЛABгкЕуEЃЎ 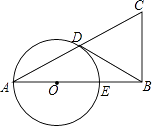
ЃЈ1ЃЉЧѓжЄЃКACAD=ABAEЃЛ
ЃЈ2ЃЉШчЙћBDЪЧЁбOЕФЧаЯпЃЌDЪЧЧаЕуЃЌEЪЧOBЕФжаЕуЃЌЕБBC=2ЪБЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњЕФПЮЭтдФЖСЧщПіЃЌОЭЁАЮвзюЯВАЎЕФПЮЭтЖСЮяЁБЖдЮФбЇЁЂвеЪѕЁЂПЦЦеКЭЦфЫћЫФИіРрБ№НјааСЫГщбљЕїВщЃЈУПЮЛЭЌбЇжЛбЁвЛРрЃЉЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК 
ЃЈ1ЃЉетДЮБЛЕїВщЕФбЇЩњЙВгаЖрЩйУћЃП
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛВЂдкЩШаЮЭГМЦЭМжаЃЌМЦЫуГіЁАЦфЫћРрЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєИУаЃга2400УћбЇЩњЃЌЧыФуЙРМЦИУаЃЯВАЎЁАПЦЦеРрЁБЕФбЇЩњгаЖрЩйУћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЪ§жсlЩЯЃЌвЛЖЏЕуQДгдЕуOГіЗЂЃЌбижБЯпlвдУПУыжг2ИіЕЅЮЛГЄЖШЕФЫйЖШРДЛивЦЖЏЃЌЦфвЦЖЏЗНЪНЪЧЯШЯђгввЦЖЏ1ИіЕЅЮЛГЄЖШЃЌдйЯђзѓвЦЖЏ2ИіЕЅЮЛГЄЖШЃЌгжЯђгввЦЖЏ3ИіЕЅЮЛГЄЖШЃЌдйЯђзѓвЦЖЏ4ИіЕЅЮЛГЄЖШЃЌгжЯђгввЦЖЏ5ИіЕЅЮЛГЄЖШЁ
![]()
ЃЈ1ЃЉЧѓГі5УыжгКѓЖЏЕуQЫљДІЕФЮЛжУЃЛ
ЃЈ2ЃЉШчЙћдкЪ§жсlЩЯЛЙгавЛИіЖЈЕуAЃЌЧвAгыдЕуOЯрОр20ИіЕЅЮЛГЄЖШЃЌЮЪЃКЖЏЕуQДгдЕуГіЗЂЃЌПЩФмгыЕуAжиКЯТ№ЃПШєФмЃЌдђЕквЛДЮгыЕуAжиКЯашЖрГЄЪБМфЃПШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com