
【题目】已知O为坐标原点,A,B分别在y轴、x轴正半轴上,D是x轴正半轴上一动点,AD=DE,∠ADE=α,矩形AOBC的面积为32且AC=2BC.
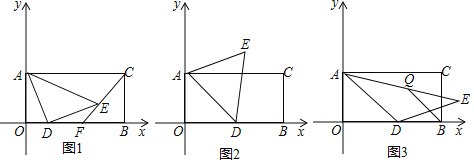
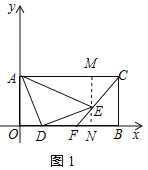
(1)如图1,当α=90°时,直线CE交x轴于点F,求证:F为OB中点;
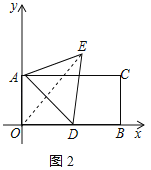
(2)如图2,当α=60°时,若D是OB中点,求E点坐标;
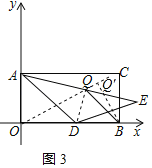
(3)如图3,当α=120°时,Q是AE的中点,求D点运动过程中BQ的最小值.
【答案】(1)见解析;(2)(2+2![]() ,2+2
,2+2![]() );(3)4
);(3)4
【解析】
(1)由题意得出BC=4,AC=8,过点E作MN⊥AC交AC于点M、交OB于点N,则四边形AONM为矩形、四边形MNBC为矩形,证明△END≌△DOA(AAS),得出OA=DN=4,EN=OD,设OD=EN=x,则ME=MN﹣EN=4﹣x,MC=AC﹣AM=AC﹣ON=AC﹣OD﹣DN=8﹣x﹣4=4﹣x,证明△CME是等腰直角三角形,得出∠MCE=45°,证出△CBF是等腰直角三角形,得出BC=BF=4,证出OF=BF即可;
(2)证明△AOD是等腰直角三角形,得出AD=4![]() ,连接OE,证明△ADE为等边三角形,得出EA=ED,证明OE垂直平分AD,由等腰三角形的性质得出∠AOE=∠DOE=45°,由勾股定理得出OE=2(
,连接OE,证明△ADE为等边三角形,得出EA=ED,证明OE垂直平分AD,由等腰三角形的性质得出∠AOE=∠DOE=45°,由勾股定理得出OE=2(![]() +
+![]() ),即可得出答案;
),即可得出答案;
(3)连接DQ、OQ,由等腰三角形的性质得出DQ⊥AE,证明A、O、D、Q四点共圆,由等腰三角形的性质得出∠DAQ=30°,由圆周角定理得出∠QOD=30°,得出Q点的运动轨迹为与x轴的一个夹角为30°的射线,当BQ⊥MN时,BQ有最小值,由含30°角的直角三角形的性质即可得出答案.
(1)证明:∵矩形AOBC的面积为32且AC=2BC,
∴S矩形AOBC=ACBC=2BCBC=2BC2=32,
∴BC=4,
∴AC=8,
过点E作MN⊥AC交AC于点M、交OB于点N,如图1所示:
则四边形AONM为矩形、四边形MNBC为矩形,
∴OA=MN=BC=4,AM+CM=ON+BN=AC=OB=8,∠END=∠DOA=90°,
∵∠ADE=90°,
∴∠ADO+∠EDN=90°,
∵∠ADO+∠DAO=90°,
∴∠EDN=∠DAO,
在△END和△DOA中,
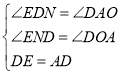 ,
,
∴△END≌△DOA(AAS),
∴OA=DN=4,EN=OD,
设OD=EN=x,
则ME=MN﹣EN=4﹣x,MC=AC﹣AM=AC﹣ON=AC﹣OD﹣DN=8﹣x﹣4=4﹣x,
∴ME=MC,
∴△CME是等腰直角三角形,
∴∠MCE=45°,
∴∠FCB=45°,
∴△CBF是等腰直角三角形,
∴BC=BF=4,
∴OF=OB﹣F=8﹣4=4,
∴OF=BF,
∴F为OB中点;
(2)解:∵D是OB中点,
∴OB=2OA=2OD=8,
∴OA=OD=4,
∴△AOD是等腰直角三角形,
∴AD=4![]() ,
,
连接OE,如图2所示:
∵AD=DE,∠ADE=60°
∴△ADE为等边三角形,
∴EA=ED,
∵AO=DO,
∴OE垂直平分AD,
∴∠AOE=∠DOE=45°,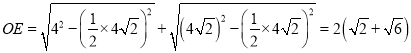
∴E点的横纵坐标为都为:![]() ×2(
×2(![]() +
+![]() )=2+2
)=2+2![]() ,
,
∴E点坐标为(2+2![]() ,2+2
,2+2![]() ),
),
(3)解:连接DQ、OQ,如图3所示:
∵AD=DE,Q是AE的中点,
∴DQ⊥AE,
∵AO⊥OD,
∴∠AOD+∠AOD=180°,
∴A、O、D、Q四点共圆,
∵∠ADE=120°,AD=DE,
∴∠DAQ=∠DEA=30°,
∴∠QOD=∠DAQ=30°,
∴Q点的运动轨迹为与x轴的一个夹角为30°的射线,
∴当BQ⊥MN时,BQ有最小值,
BQ=![]() OB=
OB=![]() ×8=4.
×8=4.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
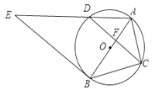
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
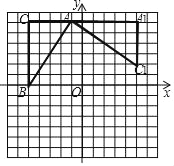
【题目】如图,△A1AC1是由△ABC绕某点P按顺时针方向旋转90°得到的,△ABC的顶点坐标分A(﹣1,6),B(﹣5,0),C(﹣5,6).
(1)求旋转中心P和点A1,C1的坐标;
(2)在所给网格中画出△A1AC1绕点P按顺时针方向旋转90°得到的图形;
(3)在所给网格中画出与△A1AC1关于点P成中心对称的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
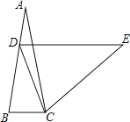
A. 80° B. 70° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
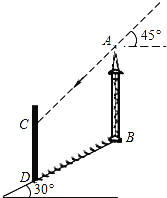
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=21,AD=8,sinB=![]() .
.
求:(1)线段DC的长;
(2)tan∠EDC的值.
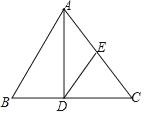
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com